题目内容
15、如图，两个等圆⊙O和⊙O′外切，过点O作⊙O′的两条切线OA、OB，A、B是切点，则∠AOB等于（ ）分析：两圆的半径分别为R和r，且R≥r，圆心距为P：外离P＞R+r；外切P=R+r；相交R-r＜P＜R+r；内切P=R-r；内含P＜R-r．
解答：解：连接O′A，OO′
则O′A⊥OA
因为OO′=2O′A
所以∠AOO′=30°
∴∠AOB=2∠AOO′=60°．
故选C．
则O′A⊥OA
因为OO′=2O′A
所以∠AOO′=30°
∴∠AOB=2∠AOO′=60°．
故选C．
点评：本题考查了由两圆位置关系来判断半径和圆心距之间数量关系的方法．
练习册系列答案
相关题目
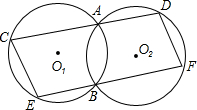于点C，点D，经过点B的直线与两圆分别交于点E，点F．若CD∥EF，求证：
（2013•桐乡市一模）如图，两个等圆⊙O1和⊙O2相交于点A、B，点C在⊙O2上，已知∠AO1B=92°，则∠ACB等于
