题目内容
（2013•桐乡市一模）如图，两个等圆⊙O1和⊙O2相交于点A、B，点C在⊙O2上，已知∠AO1B=92°，则∠ACB等于46
46
°．分析：根据等圆的性质以及圆心角定理，得出∠AO1B=∠AO2B=92°，再利用圆周角定理得出答案．
解答：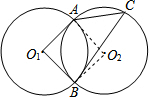
解：连接AO2，BO2，
∵两个等圆⊙O1和⊙O2相交于点A、B，点C在⊙O2上，
∴
=
，
∴∠AO1B=∠AO2B=92°，
∴∠ACB等于46°．
故答案为：46．
解：连接AO2，BO2，∵两个等圆⊙O1和⊙O2相交于点A、B，点C在⊙O2上，
∴
 |
| AB |
|
| AB |
∴∠AO1B=∠AO2B=92°，
∴∠ACB等于46°．
故答案为：46．
点评：此题主要考查了相交两圆的性质以及圆周角定理和圆心角定理，根据已知得出∠AO1B=∠AO2B=92°是解题关键．
练习册系列答案
相关题目