题目内容
（创新探究题）如图所示，已知E，F分别是矩形ABCD的边BC，CD上两点，连接AE，BF，请你再从下面四个反映图中边角关系的式子：①AB=BC；②BE=CF；③AE=BF；④∠AEB=∠BFC中选出两个作为已知条件，一个作为结论，组成一个命题，并证明这个命题是否正确（只需写出一种情况）．
答案不唯一，符合要求即可．
如：已知E，F分别是矩形ABCD边BC，CD上两点，
连接AE，BF，AB=BC，AE=BF，
求证：∠AEB=∠BFC．
证明：∵四边形ABCD是矩形，
∴∠ABE=∠BCF=90度．
又∵AB=BC，AE=BF，
∴Rt△ABE≌Rt△BCF，
∴∠AEB=∠BFC．
如：已知E，F分别是矩形ABCD边BC，CD上两点，
连接AE，BF，AB=BC，AE=BF，
求证：∠AEB=∠BFC．
证明：∵四边形ABCD是矩形，
∴∠ABE=∠BCF=90度．
又∵AB=BC，AE=BF，
∴Rt△ABE≌Rt△BCF，
∴∠AEB=∠BFC．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
40、（创新探究题）如图所示，已知E，F分别是矩形ABCD的边BC，CD上两点，连接AE，BF，请你再从下面四个反映图中边角关系的式子：①AB=BC；②BE=CF；③AE=BF；④∠AEB=∠BFC中选出两个作为已知条件，一个作为结论，组成一个命题，并证明这个命题是否正确（只需写出一种情况）．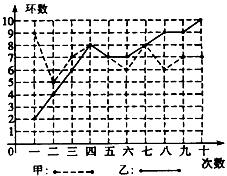
（创新探究题）甲，乙两人在相同条件下各射靶10次，每次射靶的成绩情况如图所示，请从下列四个不同的角度对这次测试结果进行分析：