题目内容
【题目】如图,一次函数y=-2x+4与x轴y轴相交于A,B两点,点C在线段AB上,且∠COA=45°.
(1)求点A,B的坐标;
(2)求△AOC的面积;
(3)直线OC上有一动点D,过点D作直线l(不与直线AB重合)与x,y轴分别交于点E,F,当△OEF与△ABO全等时,求直线EF的解析式.
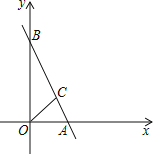
【答案】(1)A(2,0);B(0,4);(2)S△AOC=![]() ;(3)直线EF的解析式为y=-
;(3)直线EF的解析式为y=-![]() x+2或y=-2x-4或y=2x-4或-2x+4或y=-
x+2或y=-2x-4或y=2x-4或-2x+4或y=-![]() x-2或y=
x-2或y=![]() x-2或y=
x-2或y=![]() x+2.
x+2.
【解析】
(1)求出x=0时y的值和y=0时x的值即可得;
(2)设C(a,-2a+4),作CM⊥OA,由∠COA=45°知OM=CM,据此可得a=-2a+4,求出a的值后得出CM=OM=![]() ,再根据三角形面积公式可得答案;
,再根据三角形面积公式可得答案;
(3)分E、F在x、y轴的正半轴和负半轴的情况,依据△AOB≌△F1OE1、△AOB≌△E2OF2、△AOB≌△F3OE3得出OE、OF的长,从而得出点E和点F的坐标,再利用待定系数法求解可得.
解:(1)在直线y=-2x+4中,当x=0时y=4,
则B(0,4),
当y=0时,-2x+4=0,
解得x=2,
则A(2,0);
(2)设C(a,-2a+4),
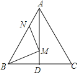
如图1,过点C作CM⊥OA于点M,
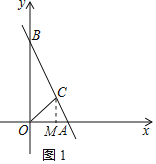
∵∠COA=45°,
∴OM=CM,
则a=-2a+4,
解得a=![]() ,
,
∴CM=OM=![]() ,
,
∴S△AOC=![]() OACM=
OACM=![]() ×2×
×2×![]() =
=![]() ;
;
(3)设直线EF解析式为y=kx+b,
如图2,
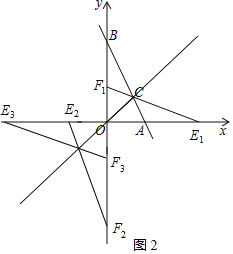
①当△AOB≌△F1OE1时,OB=OE1=4,OA=OF1=2,
则E1(4,0),F1(0,2),
代入y=kx+b得![]() ,
,
解得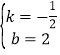 ,
,
此时直线![]() x+2,
x+2,
同理直线EF关于x轴的对称直线y=![]() x-2也符合题意;
x-2也符合题意;
②当△AOB≌△E2OF2时,OB=OF2=4,OA=OE2=2,
则E2(-2,0),F2(0,-4),
代入y=kx+b,得:![]() ,
,
解得![]()
此时直线EF解析式为y=-2x-4,
同理直线EF关于y轴的对称直线y=2x-4和关于x轴的对称直线y=-2x+4也符合要求;
③当△AOB≌△F3OE3时,OB=OE3=4,OA=OF3=2,
则E1(-4,0),F1(0,-2),
代入y=kx+b,得:![]() ,
,
解得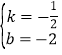 ,
,
此时直线EF解析式为y=-![]() x-2,
x-2,
同理直线EF关于x轴的对称直线y=![]() x+2也符合要求;
x+2也符合要求;
综上,直线EF的解析式为y=-![]() x+2或y=-2x-4或y=2x-4或-2x+4或y=-
x+2或y=-2x-4或y=2x-4或-2x+4或y=-![]() x-2或y=
x-2或y=![]() x-2或y=
x-2或y=![]() x+2.
x+2.