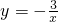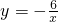题目内容
 如图,在双曲线y=
如图,在双曲线y=| 16 |
| x |
(2+2
,-2+2
)
| 5 |
| 5 |
(2+2
,-2+2
)
.| 5 |
| 5 |
分析:先根据点A1在双曲线y=
的一支上正好构成正方形,求出点A1的坐标为,再根据点A2在双曲线y=
的一支上正好构成正方形,可设点A2的坐标为(4+m,m),再代入反比例函数的解析式,求出m的值即可.
| 16 |
| x |
| 16 |
| x |
解答:解:∵双曲线y=
的一支上有点A1,正好构成正方形,
∴点A1的坐标为(4,4),
∵双曲线y=
的一支上有点A2,正好构成正方形,
∴设构成的正方形边长为m,则点A2的坐标为(4+m,m),
∴m=
,
解得:m1=-2+2
,m2=-2-2
(不合题意舍去),
∴点A2的坐标为(2+2
,-2+2
);
故答案为;(2+2
,-2+2
).
| 16 |
| x |
∴点A1的坐标为(4,4),
∵双曲线y=
| 16 |
| x |
∴设构成的正方形边长为m,则点A2的坐标为(4+m,m),
∴m=
| 16 |
| 4+m |
解得:m1=-2+2
| 5 |
| 5 |
∴点A2的坐标为(2+2
| 5 |
| 5 |
故答案为;(2+2
| 5 |
| 5 |
点评:此题考查了反比例函数综合,用到的知识点是正方形的性质、反比例函数的图象与性质,关键是根据正方形的性质设出点A2的坐标,注意把不合题意得解舍去.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
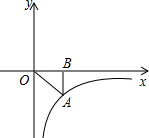 如图,在双曲线上取一点A向x轴引垂线,垂足为B,连接OA,若△AOB的面积为3,则双曲线的函数关系式为( )
如图,在双曲线上取一点A向x轴引垂线,垂足为B,连接OA,若△AOB的面积为3,则双曲线的函数关系式为( )A、y=
| ||
B、y=-
| ||
C、y=
| ||
D、y=-
|
 如图,在双曲线上取一点A向x轴引垂线,垂足为B,连接OA,若△AOB的面积为3,则双曲线的函数关系式为
如图,在双曲线上取一点A向x轴引垂线,垂足为B,连接OA,若△AOB的面积为3,则双曲线的函数关系式为