Question

【题目】已知，平分，平分．

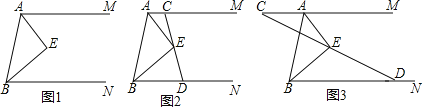
（1）求的度数；

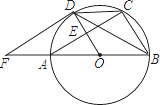
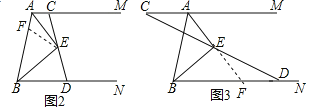
（2）如图2，过点的直线交射线于点，交射线于点，求证：；

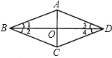
（3）如图3，过点的直线交射线的反向延长线于点，交射线于点，，，，求的面积．

Answer 1

【答案】（1）90°；（2）见解析；（3）8

【解析】

（1）根据平行线的性质得到∠BAM+∠ABN=180°，根据角平分线的定义得到∠BAE=∠BAM，∠ABE=∠ABN，于是得到结论；
（2）在AB上截取AF=AC，连接EF，根据全等三角形的性质得到∠AEC=∠AEF，BF=BD，等量代换即可得到结论；
（3）延长AE交BD于F，根据等腰三角形的性质得到AB=BF=5，AE=EF，根据全等三角形的性质得到DF=AC=3，设S△BEF=S△ABE=5x，S△DEF=S△ACE=3x，根据S△ABE-S△ACE=2，即可得到结论．

解：（1）∵AM∥BN，
∴∠BAM+∠ABN=180°，
∵AE平分∠BAM，BE平分∠ABN，
∴∠BAE=∠BAM，∠ABE=∠ABN，
∴∠BAE+∠ABE=（∠BAM+∠ABN）=90°，
∴∠AEB=90°；
（2）在AB上截取AF=AC，连接EF，
在△ACE与△AFE中，

，

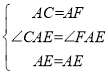∴△ACE≌△AFE，
∴∠AEC=∠AEF，
∴∠AEB=90°，
∴∠AEF+∠BEF=∠AEC+∠BED=90°，
∴∠FEB=∠DEB，
在△BFE与△BDE中，

，

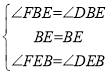∴△BFE≌△BDE（ASA），
∴BF=BD，
∵AB=AF+BF，
∴AC+BD=AB；
（3）延长AE交BD于F，
∵∠AEB=90°，
∴BE⊥CD，
BE平分∠ABN，
∴AB=BF=5，AE=EF，
∵AM∥BN，
∴∠C=∠EDF，
在△ACE与△FDE中，

，

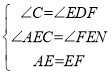∴△ACE≌△FDE（AAS），
∴DF=AC=3，
∵BF=5，
∴设S△BEF=S△ABE=5x，S△DEF=S△ACE=3x，
∵S△ABE-S△ACE=2，
∴5x-3x=2，
∴x=1，
∴△BDE的面积=8．