题目内容
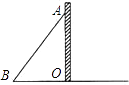
【题目】将一张矩形纸条ABCD按如图所示折叠,若折叠角∠FEC=64°. 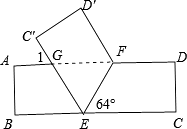
(1)求∠1的度数;
(2)求证:△EFG是等腰三角形.
【答案】
(1)解:∵∠GEF=∠FEC=64°,
∴∠BEG=180°﹣64°×2=52°
∵AD∥BC,
∴∠1=∠BEG=52°
(2)证明:∵AD∥BC,
∴∠GFE=∠FEC
∴∠GEF=∠GFE
∴GE=GF,
∴△EFG是等腰三角形
【解析】(1)根据翻折变换的性质求出∠GEF的度数,从而求出∠GEB的度数,再根据平行线的性质求出∠1;(2)根据AD∥BC得到∠GFE=∠FEC,根据翻折不变性得到∠GEF=∠GFE,由等角对等边得到GE=GF.
【考点精析】根据题目的已知条件,利用翻折变换(折叠问题)的相关知识可以得到问题的答案,需要掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目