题目内容
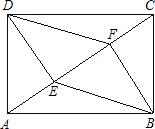 如图,一块长方形场地ABCD的长AB为50
如图,一块长方形场地ABCD的长AB为50| 2 |
分析:此题关键是求出四边形EDFB的面积,而面积的求出可由原矩形面积减去外围四个三角形的面积,外围四个三角形面积都相等,只要求出一个即可.
解答:解:设B、D到AB的垂线段长为h.
∵AD=BC,AD∥BC,且DE⊥AC,BF⊥AC,
∴△AED≌△BCF.
同理△AEB≌△DCF.
∴AE=CF,S△AED=S△BCF=S△AEB=S△DCF.
又在△ACB中,tan∠ACB=
=
=
,且∠DAC=∠ACB,
∴在△AED中,tan∠DAE=
=
,∴DE=
AE.
又AE2+DE2=AD2,∴AE2=
,即AE=
,DE=
m.
∴S△ADE=
×AE×DE=
m2.
∴S△AED+S△BCF+S△AEB+S△DCF=
m2.
∴S四边形DEBF=S矩形ABCD-
=2500
-
=
m2.
又花草的价格是每平方米180元,所以共需
×180≈212132.0344≈2.12×105元.
∵AD=BC,AD∥BC,且DE⊥AC,BF⊥AC,
∴△AED≌△BCF.
同理△AEB≌△DCF.
∴AE=CF,S△AED=S△BCF=S△AEB=S△DCF.
又在△ACB中,tan∠ACB=
| AB |
| BC |
50
| ||
| 50 |
| 2 |
∴在△AED中,tan∠DAE=
| DE |
| AE |
| 2 |
| 2 |
又AE2+DE2=AD2,∴AE2=
| 2500 |
| 3 |
50
| ||
| 3 |
50
| ||
| 3 |
∴S△ADE=
| 1 |
| 2 |
1250
| ||
| 3 |
∴S△AED+S△BCF+S△AEB+S△DCF=
5000
| ||
| 3 |
∴S四边形DEBF=S矩形ABCD-
5000
| ||
| 3 |
| 2 |
5000
| ||
| 3 |
2500
| ||
| 3 |
又花草的价格是每平方米180元,所以共需
2500
| ||
| 3 |
点评:此题主要考查平行四边形的基本性质,以及勾股定理的应用,难易适中.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
 问题解决:如图是一块长方形ABCD的运动场地,长AD=101m,宽AB=52m,从B,C两处入口的两条小路宽度相等,两条小路汇合处的路宽为B,C处入口宽的2倍,其余部分种植草坪,若草坪面积为5049m2,求B、C处入口小路的宽.
问题解决:如图是一块长方形ABCD的运动场地,长AD=101m,宽AB=52m,从B,C两处入口的两条小路宽度相等,两条小路汇合处的路宽为B,C处入口宽的2倍,其余部分种植草坪,若草坪面积为5049m2,求B、C处入口小路的宽. 如图是一块长方形ABCD的场地,长AB=62m,宽AD=41m,从A、B两处入口的路宽都为1m,两小路汇合处路宽为2m,其余部分种植草坪,则草坪面积为( )
如图是一块长方形ABCD的场地,长AB=62m,宽AD=41m,从A、B两处入口的路宽都为1m,两小路汇合处路宽为2m,其余部分种植草坪,则草坪面积为( )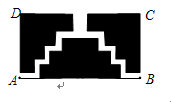
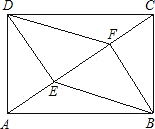 如图,一块长方形场地ABCD的长AB为50
如图,一块长方形场地ABCD的长AB为50 m,宽AD为50m,DE⊥AC于E,BF⊥AC于F,连接BE,DF.现计划在四边形DEBF区域内种植一种花草,已知该种花草的价格是180元/m2,若把四边形DEBF区域种满这种花草,约需多少元?(结果保留3位有效数字)
m,宽AD为50m,DE⊥AC于E,BF⊥AC于F,连接BE,DF.现计划在四边形DEBF区域内种植一种花草,已知该种花草的价格是180元/m2,若把四边形DEBF区域种满这种花草,约需多少元?(结果保留3位有效数字)