题目内容
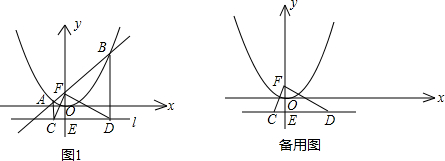
已知,如图1,过点E(0,-1)作平行于x轴的直线l,抛物线y= x2上的两点A、B的横坐标分别为-1和4,直线AB交y轴于点F,过点A、B分别作直线l的垂线,垂足分别为点C、D,连接CF、DF.
x2上的两点A、B的横坐标分别为-1和4,直线AB交y轴于点F,过点A、B分别作直线l的垂线,垂足分别为点C、D,连接CF、DF.
(1)求点A、B、F的坐标;
(2)求证:CF⊥DF;
(3)点P是抛物线y= x2对称轴右侧图象上的一动点,过点P作PQ⊥PO交x轴于点Q,是否存在点P使得△OPQ与△CDF相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
x2对称轴右侧图象上的一动点,过点P作PQ⊥PO交x轴于点Q,是否存在点P使得△OPQ与△CDF相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.

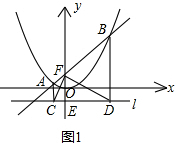 解:
解:(1)方法一:如图1,当x=-1时,y=
 ;当x=4时,y=4
;当x=4时,y=4∴A(-1,
 )
)B(4,4)
设直线AB的解析式为y=kx+b
则
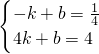
解得
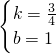
∴直线AB的解析式为y=
 x+1
x+1当x=0时,y=1∴F(0,1)
方法二:求A、B两点坐标同方法一,如图2,作FG⊥BD,AH⊥BD,垂足分别为G、H,交y轴于点N
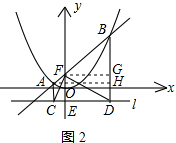 ,则四边FOMG和四边形NOMH均为矩形,设FO=x
,则四边FOMG和四边形NOMH均为矩形,设FO=x∵△BGF∽△BHA
∴
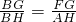
∴
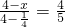
解得x=1
∴F(0,1)
(2)证明:方法一:在Rt△CEF中,CE=1,EF=2,
根据勾股定理得:CF2=CE2+EF2=12+22=5,
∴CF=

在Rt△DEF中,DE=4,EF=2
∴DF2=DE2+EF2=42+22=20
∴DF=2

由(1)得C(-1,-1),D(4,-1)
∴CD=5
∴CD2=52=25
∴CF2+DF2=CD2
∴∠CFD=90°
∴CF⊥DF
方法二:由(1)知AF=
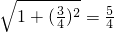 ,AC=
,AC=
∴AF=AC
同理:BF=BD
∴∠ACF=∠AFC
∵AC∥EF
∴∠ACF=∠CFO
∴∠AFC=∠CFO
同理:∠BFD=∠OFD
∴∠CFD=∠OFC+∠OFD=90°
即CF⊥DF
(3)存在.
解:如图3,作PM⊥x轴,垂足为点M
又∵PQ⊥OP
∴Rt△OPM∽Rt△OQP

∴
 ∴
∴
设P(x,
 x2)(x>0),
x2)(x>0),则PM=
 x2,OM=x
x2,OM=x①当Rt△QPO∽Rt△CFD时,

∴
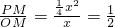
解得x=2∴P1(2,1)
②当Rt△OPQ∽Rt△CFD时,
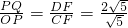 =2
=2∴
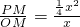 =2
=2解得x=8
∴P2(8,16)
综上,存在点P1(2,1)、P2(8,16)使得△OPQ与△CDF相似.
分析:(1)有两种方法,方法一是传统的点的待定系数法,方法二,通过作辅助线,构造△BGF∽△BHA由比例关系求出F点坐标.
(2)也有两种方法,方法一,在Rt△CEF中算出△DEF边长利用勾股定理证明CF⊥DF;方法二利用几何关系求出∠CFD=90°;
(3)求存在性问题,先假设存在,看是否找到符合条件的点P的坐标,此题分两种情况;(1)Rt△QPO∽Rt△CFD;(2)Rt△OPQ∽Rt△CFD,根据比例求出P点坐标.
点评:此题是一道综合性较强的题,前两问方法多,有普通的方法和新颖的方法,作合适的辅助线很重要,最后一问是探究性问题,发散思维.

练习册系列答案
相关题目

 x2上的两点A、B的横坐标分别为-1和4,直线AB交y轴于点F,过点A、B分别作直线l的垂线,垂足分别为点C、D,连接CF、DF.
x2上的两点A、B的横坐标分别为-1和4,直线AB交y轴于点F,过点A、B分别作直线l的垂线,垂足分别为点C、D,连接CF、DF. x2对称轴右侧图象上的一动点,过点P作PQ⊥PO交x轴于点Q,是否存在点P使得△OPQ与△CDF相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
x2对称轴右侧图象上的一动点,过点P作PQ⊥PO交x轴于点Q,是否存在点P使得△OPQ与△CDF相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
 x2上的两点A、B的横坐标分别为-1和4,直线AB交y轴于点F,过点A、B分别作直线l的垂线,垂足分别为点C、D,连接CF、DF.
x2上的两点A、B的横坐标分别为-1和4,直线AB交y轴于点F,过点A、B分别作直线l的垂线,垂足分别为点C、D,连接CF、DF. x2对称轴右侧图象上的一动点,过点P作PQ⊥PO交x轴于点Q,是否存在点P使得△OPQ与△CDF相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
x2对称轴右侧图象上的一动点,过点P作PQ⊥PO交x轴于点Q,是否存在点P使得△OPQ与△CDF相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.