جâؤ؟ؤعبف
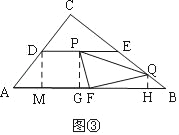
،¾جâؤ؟،؟بçح¼£¬شع،÷ABCضذ£¬،دC=90،م£¬AC=6cm£¬BC=8cm£¬D،¢E،¢F·ض±ًتاAC،¢BC،¢ABµؤضذµم£¬ء¬½سDE£®µمP´سµمD³ِ·¢£¬رطDE·½دٍشبثظشث¶¯£»ح¬ت±£¬µمQ´سµمE³ِ·¢£¬رطEB·½دٍشبثظشث¶¯£¬ء½صكثظ¶ب¾ùخھ1cm/s£»µ±ئنضذز»µمح£ض¹شث¶¯ت±£¬ءيحâز»µمز²ح£ض¹شث¶¯£®ء¬½سPQ،¢PF£¬ةèشث¶¯ت±¼نخھts£¨0£¼t£¼4£©£®½â´ًدآءذختجâ£؛
£¨1£©µ±tخھ؛خضµت±£¬،÷EPQخھµبرüب½اذخ£؟
£¨2£©بçح¼¢ظ£¬ةèثؤ±كذخPFBQµؤأو»خھycm2£¬اَyسëtض®¼نµؤ؛¯ت¹طدµت½£»
£¨3£©µ±tخھ؛خضµت±£¬ثؤ±كذخPFBQµؤأو»سë،÷ABCµؤأو»ض®±بخھ2£؛5£؟
£¨4£©بçح¼¢ع£¬ء¬½سFQ£¬تا·ٌ´وشعؤ³ز»ت±؟ج£¬ت¹µأPFسëQF»¥دà´¹ض±£؟بô´وشع£¬اَ³ِ´ثت±tµؤضµ£»بô²»´و£¬اëثµأ÷ہيسة£®

،¾´ً°¸،؟£¨1£©µ±t=![]() ت±£¬،÷EPQخھµبرüب½اذخ£»£¨2£©y=
ت±£¬،÷EPQخھµبرüب½اذخ£»£¨2£©y=![]() £»£¨3£©1£»£¨4£©t=
£»£¨3£©1£»£¨4£©t=![]() ت±£¬PFسëQF»¥دà´¹ض±.
ت±£¬PFسëQF»¥دà´¹ض±.
،¾½âخِ،؟
£¨1£©¸ù¾ف¹´¹ة¶¨ہياَ³ِAB=10£¬سةDEتاضذخ»دك؟ةضھDE=5£¬،÷EPQخھµبرüب½اذخض»ذèPE=EQ£¬¼´t=5-t,½â·½³ج¼´؟ة.£¨2£©¹P×÷PH،حBCسعH£¬ء¬½سFE£¬سةsin،دPEH=![]() £¬؟ةضھPH=
£¬؟ةضھPH=![]() £¬¼´،÷EQPµؤ¸ك£¬¸ù¾ف،÷CDE؟ةاَ³ِDE±كµؤ¸ك£¬¼´،÷PEF؛ح،÷EFBµؤ¸ك£¬¸ù¾فy=S،÷PEF+S،÷EFB©پS،÷EQP£¬¼´؟ةµأ´ً°¸£»£¨3£©دباَ³ِ،÷ABCµؤأو»£¬¸ù¾ف£¨2£©ثùµأ¹طدµت½¼°زرضھأو»±ب£¬ءذ·½³ج¼´؟ةµأ´ً°¸.£¨4£©بçح¼¢غ¹P×÷PG،حABسعG£¬¹Q×÷QH،حABسعH£¬¹D×÷DM،حABسعM£¬سة¹´¹ة¶¨ہي؟ةضھAMµؤ³¤£¬،÷BHQضذ£¬ہûسأ،دBµؤب½ا؛¯تضµ؟ةµأBH،¢QHµؤ³¤£¬سةPF،حFQ£¬؟ةض¤أ÷،÷PGF،×،÷FHQ£¬¸ù¾ف¶شس¦±كµؤ¹طدµءذ³ِ·½³ج¼´؟ةاَµأtµؤضµ.
£¬¼´،÷EQPµؤ¸ك£¬¸ù¾ف،÷CDE؟ةاَ³ِDE±كµؤ¸ك£¬¼´،÷PEF؛ح،÷EFBµؤ¸ك£¬¸ù¾فy=S،÷PEF+S،÷EFB©پS،÷EQP£¬¼´؟ةµأ´ً°¸£»£¨3£©دباَ³ِ،÷ABCµؤأو»£¬¸ù¾ف£¨2£©ثùµأ¹طدµت½¼°زرضھأو»±ب£¬ءذ·½³ج¼´؟ةµأ´ً°¸.£¨4£©بçح¼¢غ¹P×÷PG،حABسعG£¬¹Q×÷QH،حABسعH£¬¹D×÷DM،حABسعM£¬سة¹´¹ة¶¨ہي؟ةضھAMµؤ³¤£¬،÷BHQضذ£¬ہûسأ،دBµؤب½ا؛¯تضµ؟ةµأBH،¢QHµؤ³¤£¬سةPF،حFQ£¬؟ةض¤أ÷،÷PGF،×،÷FHQ£¬¸ù¾ف¶شس¦±كµؤ¹طدµءذ³ِ·½³ج¼´؟ةاَµأtµؤضµ.
£¨1£©،دC=90،م£¬AC=6cm£¬BC=8cm£¬
،àAB=10cm£¬
سةجâزâµأ£؛DP=EQ=t£¬
،كDخھACµؤضذµم£¬EخھBCµؤضذµم£¬
،àDE=![]() AB=5cm£¬
AB=5cm£¬
µ±EP=EQت±£¬5©پt=t£¬
t=![]() £¬
£¬
¼´µ±t=![]() ت±£¬،÷EPQخھµبرüب½اذخ£»
ت±£¬،÷EPQخھµبرüب½اذخ£»
£¨2£©بçح¼¢ع£¬¹P×÷PH،حBCسعH£¬ء¬½سFE£¬
sin،دPEH=![]() £¬
£¬
،à![]() £¬
£¬
،àPH=![]() £¬
£¬
ةè،÷DCEضذ£¬DE±كةدµؤ¸كخھh£¬
![]() ،ء3،ء4=
،ء3،ء4=![]() ،ء5h£¬h=
،ء5h£¬h=![]() £¬
£¬
،ày=S،÷PEF+S،÷EFB©پS،÷EQP£¬
=![]() ،ء
،ء![]() PE+
PE+![]() ،ء
،ء![]() FB©پ
FB©پ![]() EQPH£¬
EQPH£¬
=![]() £¨5©پt£©+
£¨5©پt£©+![]() ،ء5©پ
،ء5©پ![]() £¬
£¬
=![]() ©پ
©پ![]() t+12£»
t+12£»
£¨3£©،ك![]() £¬
£¬
،à5Sثؤ±كذخPFBQ=2S،÷ABC£¬
،à5£¨![]() ©پ
©پ![]() t+12£©=2،ء
t+12£©=2،ء![]() ،ء6،ء8£¬
،ء6،ء8£¬
t2©پ9t+8=0£¬
t1=1£¬t2=8£¨ةل£©£»
£¨4£©بçح¼¢غ£¬¹P×÷PG،حABسعG£¬¹Q×÷QH،حABسعH£¬¹D×÷DM،حABسعM£¬
سة£¨3£©ضھ£؛PG=DM=![]() £¬
£¬
Rt،÷ADMضذ£¬،كAD=3£¬
،àAM=![]() £¬
£¬
،àFG=5©پ![]() ©پt=
©پt=![]() ©پt£¬
©پt£¬
Rt،÷QHBضذ£¬BQ=4©پt£¬
sin،دB=![]() £¬
£¬
،àQH=![]() £¬
£¬
،àBH=![]() £¬
£¬
،àFH=5©پBH=![]() £¬
£¬
،كPF،حFQ£¬
ز×µأ،÷PGF،×،÷FHQ£¬
،à![]() £¬
£¬
،àPGQH=FHGF£¬
،à![]() £¬
£¬
4t2©پ11t=0£¬
t1=0£¨ةل£©£¬t2=![]() £®
£®
،൱t=![]() ت±£¬PFسëQF»¥دà´¹ض±£®
ت±£¬PFسëQF»¥دà´¹ض±£®

،¾جâؤ؟،؟شعث®¹ûدْتغحْ¼¾£¬ؤ³ث®¹ûµê¹؛½ّز»سإضتث®¹û£¬½ّ¼غخھ 20 شھ/ا§؟ث£¬تغ¼غ²»µحسع 20 شھ/ا§؟ث£¬از²»³¬¹ 32 شھ/ا§؟ث£¬¸ù¾فدْتغاé؟ِ£¬·¢دض¸أث®¹ûز»جىµؤدْتغء؟ y£¨ا§؟ث£©سë¸أجىµؤتغ¼غ x£¨شھ/ا§؟ث£©آْ×مبçدآ±يثùت¾µؤز»´خ؛¯ت¹طدµ£®
دْتغء؟ y£¨ا§؟ث£© | ، | 34.8 | 32 | 29.6 | 28 | ، |
تغ¼غ x£¨شھ/ا§؟ث£© | ، | 22.6 | 24 | 25.2 | 26 | ، |
(1)ؤ³جىصâضضث®¹ûµؤتغ¼غخھ 23.5 شھ/ا§؟ث£¬اَµ±جى¸أث®¹ûµؤدْتغء؟£®
(2)بç¹ûؤ³جىدْتغصâضضث®¹û»ٌہû 150 شھ£¬ؤاأ´¸أجىث®¹ûµؤتغ¼غخھ¶àةظشھ£؟
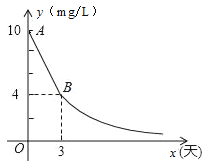
،¾جâؤ؟،؟»·±£¾ض¶شؤ³ئَزµإإخغاé؟ِ½ّذذ¼ى²â£¬½ل¹ûدشت¾£؛ثùإإخغث®ضذءٍ»¯خïµؤإ¨¶ب³¬±ê£¬¼´ءٍ»¯خïµؤإ¨¶ب³¬¹×î¸كشتذيµؤ1.0 mg/L£®»·±£¾ضزھاَ¸أئَزµء¢¼´صû¸ؤ£¬شع15جىزشؤع£¨؛¬15جى£©إإخغ´ï±ê£®صû¸ؤ¹³جضذ£¬ثùإإخغث®ضذءٍ»¯خïµؤإ¨¶بy£¨mg/L£©سëت±¼نx£¨جى£©µؤ±ن»¯¹وآةبçح¼ثùت¾£¬ئنضذدك¶خAB±يت¾ا°3جىµؤ±ن»¯¹وآة£¬ئنضذµع3جىت±ءٍ»¯خïµؤإ¨¶ب½µخھ4 mg/L£®´سµع3جىئًثùإإخغث®ضذءٍ»¯خïµؤإ¨¶بyسëت±¼نxآْ×مدآأو±ي¸ٌضذµؤ¹طدµ£؛
ت±¼نx£¨جى£© | 3 | 4 | 5 | 6 | 8 | ،، |
ءٍ»¯خïµؤإ¨y£¨mg/L£© | 4 | 3 | 2.4 | 2 | 1.5 |
£¨1£©اَصû¸ؤ¹³جضذµ±0،ـx<3ت±£¬ءٍ»¯خïµؤإ¨¶بyسëت±¼نxµؤ؛¯ت±ي´ïت½£»
£¨2£©اَصû¸ؤ¹³جضذµ±x،ف3ت±£¬ءٍ»¯خïµؤإ¨¶بyسëت±¼نxµؤ؛¯ت±ي´ïت½£»
£¨3£©¸أئَزµثùإإخغث®ضذءٍ»¯خïµؤإ¨¶ب£¬ؤـ·ٌشع15جىزشؤع²»³¬¹×î¸كشتذيµؤ1.0 mg/L£؟خھت²أ´£؟