Question

【题目】（12分）如图，在平面直角坐标系xOy中，抛物线过点A（0，4）和C（8，0），P（t，0）是x轴正半轴上的一个动点，M是线段AP的中点，将线段MP绕点P顺时针旋转90°得线段PB，过点B作x轴的垂线，过点A作y轴的垂线，两直线交于点D．

（1）求b、c的值；

（2）当t为何值时，点D落在抛物线上；

（3）是否存在t，使得以A，B，D为顶点的三角形与△AOP相似？若存在，求此时t的值；若不存在，请说明理由．

Answer 1

【答案】（1）b=，c=4；（2）t=3；（3）t=或．

【解析】

试题分析：（1）将A、C两点坐标代入抛物线，求出b，c的值即可；

（2）先求得M的坐标，进而求出点D的坐标，然后将D（t+2，4）代入（1）中的抛物线的解析式，即可求出t的值；

（3）由于t=8时，点B与点D重合，△ABD不存在，所以分0＜t＜8和t＞8两种情况进行讨论，在每一种情况下，当以A、B、D为顶点的三角形与△PEB相似时，又分两种情况：△BEP∽△ADB与△PEB∽△ADB，根据相似三角形对应边的比相等列出比例式，求解即可．

试题解析：（1）∵抛物线过点A（0，4）和C（8，0），

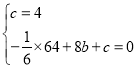∴，解得：，∴b=，c=4；

（2）∵∠AOP=∠PEB=90°，∠OAP=∠EPB=90°﹣∠APO，∴△AOP∽△PEB且相似比为=2，∵AO=4，∴PE=2，OE=OP+PE=t+2，又∵DE=OA=4，∴点D的坐标为（t+2，4），∴点D落在抛物线上时，有，解得t=3或t=﹣2，∵t＞0，∴t=3．故当t为3时，点D落在抛物线上；

（3）存在t，能够使得以A、B、D为顶点的三角形与△AOP相似，理由如下：

①当0＜t＜8时，如图1．

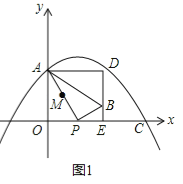
若△POA∽△ADB，则PO：AD=AO：BD，即t：（t+2）=4：（4﹣t），整理得：，∴t无解；

若△POA∽△BDA，同理，解得（负值舍去）；

②当t＞8时，如图2．

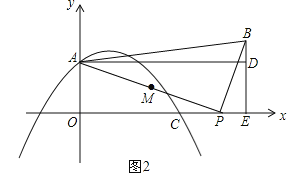
若△POA∽△ADB，则PO：AD=AO：BD，即t：（t+2）=4：（t﹣4），解得t=（负值舍去）；

若△POA∽△BDA，同理，解得t无解．

综上可知，当t=或时，以A、B、D为顶点的三角形与△AOP相似．