题目内容
如图,已知点A是函数y=x与y= 的图象在第一象限内的交点,点B在x轴负半轴上,且OA=OB,则△AOB的面积为( )
的图象在第一象限内的交点,点B在x轴负半轴上,且OA=OB,则△AOB的面积为( )

A.2 B. C.2
C.2 D.4
D.4
【答案】
C
【解析】
试题分析:先根据点A是函数y=x与y=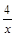 的图象在第一象限内的交点求得点A的坐标,再根据OA=OB及勾股定理即可求得点B的坐标,最后根据三角形的面积公式求解即可.
的图象在第一象限内的交点求得点A的坐标,再根据OA=OB及勾股定理即可求得点B的坐标,最后根据三角形的面积公式求解即可.
解:∵点A是函数y=x与y=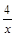 的图象在第一象限内的交点,
的图象在第一象限内的交点,
∴x=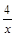 ,解得x=2(舍负),则A(2,2),
,解得x=2(舍负),则A(2,2),
又∵OA=OB=2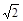 ,
,
∴B(-2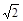 ,0),
,0),
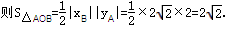
故选C.
考点:函数图象上的点的坐标的特征,勾股定理,三角形的面积公式
点评:此类问题是初中数学的重点,是中考中比较常见的知识点,一般难度不大,需熟练掌握.

练习册系列答案
相关题目
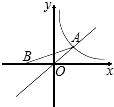 如图,已知点A是函数y=x与y=
如图,已知点A是函数y=x与y=

 的图象在第一象限内的交点,点B在x轴负半轴上,且OA=OB,则△AOB的面积为( )
的图象在第一象限内的交点,点B在x轴负半轴上,且OA=OB,则△AOB的面积为( )

 如图,已知点A是函数y=x与y=
如图,已知点A是函数y=x与y= 的图象在第一象限内的交点,点B在x轴负半轴上,且OA=OB,则△AOB的面积为
的图象在第一象限内的交点,点B在x轴负半轴上,且OA=OB,则△AOB的面积为