题目内容
探索三角形的内角与外角平分线:
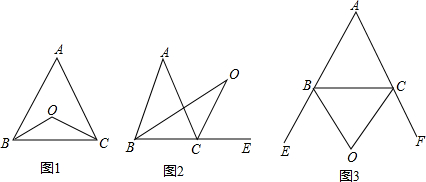
(1)已知,如图1,在△ABC中,两内角平分线,BO平分∠ABC,CO平分∠ACB,若∠A=50°,则∠BOC= _________ ;此时∠A与∠BOC有怎样的关系,试说明理由.
(2)已知,如图2,在△ABC中,一内角平分线BO平分∠ABC,一外角平分线CO平分∠ACE,若∠A=50°,则∠BOC= _________ ;此时∠A与∠BOC有怎样的关系,试说明理由.
(3)已知,如图3,在△ABC中,∠ABC、∠ACB的外角平分线OB、OC相交于点O,若∠A=50°,则∠BOC= _________ ;此时∠A与∠BOC有怎样的关系(不需说明理由)
(1)已知,如图1,在△ABC中,两内角平分线,BO平分∠ABC,CO平分∠ACB,若∠A=50°,则∠BOC= _________ ;此时∠A与∠BOC有怎样的关系,试说明理由.
(2)已知,如图2,在△ABC中,一内角平分线BO平分∠ABC,一外角平分线CO平分∠ACE,若∠A=50°,则∠BOC= _________ ;此时∠A与∠BOC有怎样的关系,试说明理由.
(3)已知,如图3,在△ABC中,∠ABC、∠ACB的外角平分线OB、OC相交于点O,若∠A=50°,则∠BOC= _________ ;此时∠A与∠BOC有怎样的关系(不需说明理由)
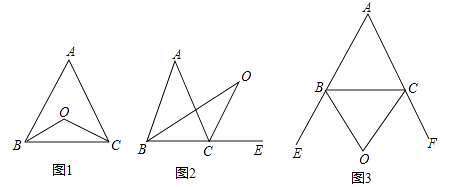
图1中:关系式: _________ ,理由: _________ ;
图2中:关系式: _________ ,理由: _________ ;
图3中:关系式: _________ ,理由: _________ 。
图2中:关系式: _________ ,理由: _________ ;
图3中:关系式: _________ ,理由: _________ 。
解:(1)∠BOC=90°+ ∠A.理由如下:
∠A.理由如下:
∵∠BOC=180°﹣∠OBC﹣∠OCB,
∴2∠BOC=360°﹣2∠OBC﹣2∠OCB,
而BO平分∠ABC,CO平分∠ACB,
∴∠ABC=2∠OBC,∠ACB=2∠OCB,
∴2∠BOC=360°﹣(∠ABC+∠ACB),
∵∠ABC+∠ACB=180°﹣∠A,
∴2∠BOC=180°+∠A,
∴∠BOC=90°+ ∠A.
∠A.
当∠A=50°,∠BOC=115°;
(2)∠BOC= ∠A.理由如下:
∠A.理由如下:
∵∠OCE=∠BOC+∠OBC,∠ACE=∠ABC+∠A,
而BO平分∠ABC,CO平分∠ACE,
∴∠ACE=2∠OCE,∠ABC=2∠OBC,
∴2∠BOC+2∠OBC=∠ABC+∠A,
∴2∠BOC=∠A,即∠BOC= ∠A.
∠A.
当∠A=50°,∠BOC=25°;
(3)∠BOC=90°﹣ ∠A.
∠A.
当∠A=50°,∠BOC=65°.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目