题目内容
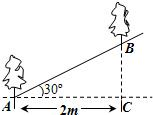如图，沿倾斜角为30°的山坡植树，要求相邻两棵树的水平距离AC为2m，求相邻两棵树的斜坡距离AB．（精确到0.1m）
分析：AB是Rt△ABC的斜边，这个直角三角形中，已知一边和一锐角，满足解直角三角形的条件，可求出AB的长．
解答：解：在Rt△ABC中，∠C=90°，∠A=30°，AC=2m，（1分）
cos∠A=
，（4分）
∴cos30°=
，（6分）
∴AB=
≈2.3（m）．（8分）
答：斜坡AB的长为2.3m．
cos∠A=
| AC |
| AB |
∴cos30°=
| 2 |
| AB |
∴AB=
| 2 |
| cos30° |
答：斜坡AB的长为2.3m．
点评：应用问题尽管题型千变万化，但关键是设法化归为解直角三角形问题，必要时应添加辅助线，构造出直角三角形．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
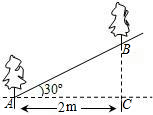如图，沿倾斜角为30°的山坡植树，要求相邻两棵树间的水平距离AC为2m，那么相邻两棵树的斜坡距离AB约为
，那么相邻两棵树的斜坡距离AB约为_________
.(结果精确到0.1
，
).
，那么相邻两棵树的斜坡距离AB约为_________
.(结果精确到0.1
，
).
