题目内容
【题目】如图,在矩形ABCD中,AD=2AB,点M、N分别在边AD、BC上,连接BM、DN.若四边形MBND是菱形,则 ![]() 等于( )
等于( ) 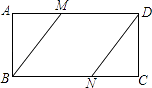
A.![]()
B.![]()
C.![]()
D.![]()
【答案】C
【解析】解:∵四边形MBND是菱形,
∴MD=MB.
∵四边形ABCD是矩形,
∴∠A=90°.
设AB=x,AM=y,则MB=2x﹣y,(x、y均为正数).
在Rt△ABM中,AB2+AM2=BM2 , 即x2+y2=(2x﹣y)2 ,
解得x= ![]() y,
y,
∴MD=MB=2x﹣y= ![]() y,
y,
∴ ![]() =
= ![]() =
= ![]() .
.
故选:C.
【考点精析】掌握勾股定理的概念和菱形的性质是解答本题的根本,需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目