��Ŀ����
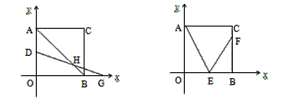
ƽ��ֱ������ϵ�У�������AOBC��ͼ��ʾ����C������Ϊ��a��a��������aʹ��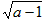 +
+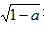 ʽ�������壬����������y=
ʽ�������壬����������y=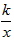 ��ͼ����C��
��ͼ����C��
��1��������������ʽ��
��2������һ��D��A��O�˶���������AD2=OD��AO�����ʱD�����ꣻ
��3������D��AO�ϡ�GΪOB���ӳ����ϵĵ㣬AD=BG������AB��DG�ڵ�H��д��AB-2HB��AD֮���������ϵ��ֱ��д������֤������
��4����ͼ����EΪ������AOBC��OB��һ�㣬��FΪBC��һ���ҡ�CAE=��FEA=60�㣬��ֱ��EF�Ľ���ʽ��
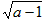 +
+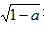 ʽ�������壬����������y=
ʽ�������壬����������y=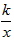 ��ͼ����C��
��ͼ����C����1��������������ʽ��
��2������һ��D��A��O�˶���������AD2=OD��AO�����ʱD�����ꣻ
��3������D��AO�ϡ�GΪOB���ӳ����ϵĵ㣬AD=BG������AB��DG�ڵ�H��д��AB-2HB��AD֮���������ϵ��ֱ��д������֤������
��4����ͼ����EΪ������AOBC��OB��һ�㣬��FΪBC��һ���ҡ�CAE=��FEA=60�㣬��ֱ��EF�Ľ���ʽ��
�⣺��1��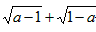 �����壬��a=1
�����壬��a=1
��C��1��1������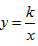 �е�k=1��
�е�k=1��
��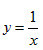
��2��OA=1��OD=1-AD
AD2=OD��AO=1����1-AD��
AD2+AD-1=0
AD=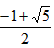
��AD��0
��AD=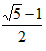 ��OD=
��OD=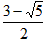
��D��0��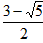 ��
��
��3��AB-2HB=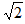 AD
AD
��4���ߡ�CAE=��FEA=60��
���OAE=30��
OA=1��
��OE=x����AE=2x
x2+12=��2x��2
��ã�x=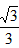 ��OE=
��OE=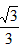 ��AE=
��AE=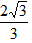
��BEF=180��-��OEA-��AEF=60��
BE=1-OE=1-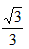 ��FE=2-
��FE=2-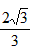 ��BF=
��BF=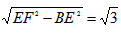 -1
-1
��E��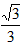 ��0�� F��1��
��0�� F��1��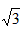 -1��
-1��
�����ʽΪy=kx+b��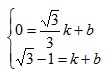 ���
���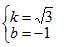
��y=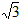 x-1��
x-1��

��ϰ��ϵ�д�
 ���źþ���Ԫ����ĩ��ϵ�д�
���źþ���Ԫ����ĩ��ϵ�д�
�����Ŀ

 ��ƽ��ֱ������ϵ�У�����O1A1B1���߳�Ϊ1��O1������ԭ�㣬ȡA1B1���е����ڶ�������O2A2B2��ȡA2B2���е�������������O3A3B3���������е��������ζ�����y��Գƣ�����������������εı߳���������1����λ���ȣ�����An���ڵ�һ�����ڣ�n��1����nΪ����������ôA2������Ϊ
��ƽ��ֱ������ϵ�У�����O1A1B1���߳�Ϊ1��O1������ԭ�㣬ȡA1B1���е����ڶ�������O2A2B2��ȡA2B2���е�������������O3A3B3���������е��������ζ�����y��Գƣ�����������������εı߳���������1����λ���ȣ�����An���ڵ�һ�����ڣ�n��1����nΪ����������ôA2������Ϊ
 ��ƽ��ֱ������ϵ�У�����O1A1B1���߳�Ϊ1��O1������ԭ�㣬ȡA1B1���е����ڶ�������O2A2B2��ȡA2B2���е�������������O3A3B3���������е��������ζ�����y��Գƣ�����������������εı߳���������1����λ���ȣ�����An���ڵ�һ�����ڣ�n��1����nΪ����������ôA2������Ϊ________��An������________��
��ƽ��ֱ������ϵ�У�����O1A1B1���߳�Ϊ1��O1������ԭ�㣬ȡA1B1���е����ڶ�������O2A2B2��ȡA2B2���е�������������O3A3B3���������е��������ζ�����y��Գƣ�����������������εı߳���������1����λ���ȣ�����An���ڵ�һ�����ڣ�n��1����nΪ����������ôA2������Ϊ________��An������________��