题目内容
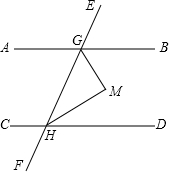 如图已知AB∥CD,EF交AB、CD于G、H,若∠BGH和∠DHG的平分线交于点M,试判断GM和HM是否垂直,并说明理由.
如图已知AB∥CD,EF交AB、CD于G、H,若∠BGH和∠DHG的平分线交于点M,试判断GM和HM是否垂直,并说明理由.
分析:根据两直线平行同旁内角互补可得∠BGH+∠DHG=180°,再由角平分线的定义不难推出∠MGH+∠MNG=90°,即得到GM与HM垂直.
解答:解:垂直.
∵AB∥CD,
∴∠BGH+∠DHG=180°,
∵∠BGH和∠DHG的平分线交于点M,
∴∠BGM=∠MGH,∠GHM=∠MHD,
∴∠MGH+∠MHG=
∠BGH+
∠DHG=
(∠BGH+∠DHG)=90°,
∴∠GMH=90°,
∴GM和HM垂直.
∵AB∥CD,
∴∠BGH+∠DHG=180°,
∵∠BGH和∠DHG的平分线交于点M,
∴∠BGM=∠MGH,∠GHM=∠MHD,
∴∠MGH+∠MHG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠GMH=90°,
∴GM和HM垂直.
点评:此题主要考查学生对平行线的性质及角平分线的定义的综合运用能力.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
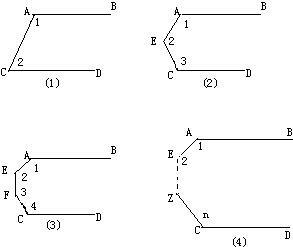 24、细观察,找规律
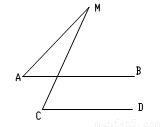
24、细观察,找规律 如图已知AB∥CD,∠A=45°,∠C=75°,则∠M=
如图已知AB∥CD,∠A=45°,∠C=75°,则∠M= 如图已知AB∥CD,∠A=∠C,BF=DE,请说明AB=CD的理由.
如图已知AB∥CD,∠A=∠C,BF=DE,请说明AB=CD的理由.