题目内容
(2005•济宁)已知⊙P的圆心坐标为(1.5,0),半径为2.5,⊙P与x轴交于A、B两点(点A在点B的左侧),与y轴的负半轴交于点D.(1)求D点的坐标;
(2)求过A、B、D三点的抛物线的解析式;
(3)设平行于x轴的直线交此抛物线于E、F两点,问:是否存在以线段EF为直径的圆O'恰好与⊙P相外切?若存在,求出其半径r及圆心O'的坐标;若不存在,请说明理由.

【答案】分析:(1)已知了圆心P坐标即圆P的半径,不难得出A、B的坐标,根据相交弦定理的推论,可得出OD2=OA•OB,即可求出OD的长,也就得出了D点的坐标.
(2)已知了A、B、D三点坐标,可用待定系数法求出抛物线的解析式.
(3)根据圆和抛物线的对称性可知:圆心O′和圆心P必在抛物线的对称轴上.本题应该分两种情况:①圆O′在x轴上方;②圆O′在x轴下方;解法一致:都是根据两圆外切的特点进行求解,由于两圆外切,那么圆心O′的纵坐标的绝对值就是两圆半径之和,可设出圆O′的半径,然后用圆O′的半径,表示出E或F的坐标,然后将E或F的坐标代入抛物线的解析式中,即可求得圆O′的半径长,也就可得出圆心O′的坐标.
解答: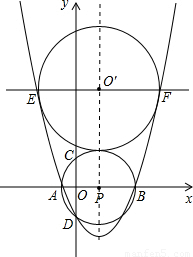 解:(1)由已知,得OA=1,OB=4,
解:(1)由已知,得OA=1,OB=4,
∴OD2=OA•OB=1×4,OD=2
∴D点的坐标为(0,-2);
(2)设过A、B、D三点多抛物线解析式为y=ax2+bx+c,把A(-1,0)、B(0,-2)的坐标代入解析式,得:

∴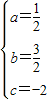
∴过点A、B、D三点多抛物线的解析式为y= x2-
x2- x-2;
x-2;
(3)存在.配方y= x2-
x2- x-2=
x-2= (x-
(x- )2-
)2-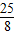
抛物线的对称轴为x= ,圆心O’应在对称轴上.分两种情况:
,圆心O’应在对称轴上.分两种情况:
①当以线段EF为直径的圆O′在x轴上方时,F( +r,
+r, +r)在抛物线y=
+r)在抛物线y= x2-
x2- x-2上,
x-2上,
∴ +r=
+r= (
( +r)2-
+r)2- (
( +r)-2,
+r)-2,
整理得4r2-8r-45=0,
解得r= 或r=-
或r=- (舍去)
(舍去)
∴半径r= .圆心O′(
.圆心O′( ,7);
,7);
②当以线段EF为直径的圆O′在x轴下方时:F( +r,-
+r,- -r)在抛物线y=
-r)在抛物线y= x2-
x2- x-2上,
x-2上,
∴- -r=
-r= (
( +r)2-
+r)2- (
( +r)-2,
+r)-2,
整理得4r2+8r-5=0,
解得r= 或r=
或r= (舍去)
(舍去)
∴半径r= ,圆心O′(
,圆心O′(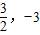 ).
).
点评:本题考查了二次函数解析式的确定、圆与圆的位置关系、抛物线与圆的对称性等知识,综合性强,难度较大.
(2)已知了A、B、D三点坐标,可用待定系数法求出抛物线的解析式.
(3)根据圆和抛物线的对称性可知:圆心O′和圆心P必在抛物线的对称轴上.本题应该分两种情况:①圆O′在x轴上方;②圆O′在x轴下方;解法一致:都是根据两圆外切的特点进行求解,由于两圆外切,那么圆心O′的纵坐标的绝对值就是两圆半径之和,可设出圆O′的半径,然后用圆O′的半径,表示出E或F的坐标,然后将E或F的坐标代入抛物线的解析式中,即可求得圆O′的半径长,也就可得出圆心O′的坐标.
解答:
 解:(1)由已知,得OA=1,OB=4,
解:(1)由已知,得OA=1,OB=4,∴OD2=OA•OB=1×4,OD=2
∴D点的坐标为(0,-2);
(2)设过A、B、D三点多抛物线解析式为y=ax2+bx+c,把A(-1,0)、B(0,-2)的坐标代入解析式,得:

∴
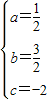
∴过点A、B、D三点多抛物线的解析式为y=
 x2-
x2- x-2;
x-2;(3)存在.配方y=
 x2-
x2- x-2=
x-2= (x-
(x- )2-
)2-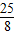
抛物线的对称轴为x=
 ,圆心O’应在对称轴上.分两种情况:
,圆心O’应在对称轴上.分两种情况:①当以线段EF为直径的圆O′在x轴上方时,F(
 +r,
+r, +r)在抛物线y=
+r)在抛物线y= x2-
x2- x-2上,
x-2上,∴
 +r=
+r= (
( +r)2-
+r)2- (
( +r)-2,
+r)-2,整理得4r2-8r-45=0,
解得r=
 或r=-
或r=- (舍去)
(舍去)∴半径r=
 .圆心O′(
.圆心O′( ,7);
,7);②当以线段EF为直径的圆O′在x轴下方时:F(
 +r,-
+r,- -r)在抛物线y=
-r)在抛物线y= x2-
x2- x-2上,
x-2上,∴-
 -r=
-r= (
( +r)2-
+r)2- (
( +r)-2,
+r)-2,整理得4r2+8r-5=0,
解得r=
 或r=
或r= (舍去)
(舍去)∴半径r=
 ,圆心O′(
,圆心O′(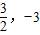 ).
).点评:本题考查了二次函数解析式的确定、圆与圆的位置关系、抛物线与圆的对称性等知识,综合性强,难度较大.

练习册系列答案
相关题目

 cm
cm cm
cm cm
cm cm
cm