题目内容
已知:sinα=
则cosα=( )
| 1 |
| 3 |
分析:根据sinα2+coaα2=1可求出coaα的值.
解答:解:∵sinα2+coaα2=1,sinα=
,
∴cosα=±
,
又∵∠α为锐角,
∴cosα=
.
故选D.
| 1 |
| 3 |
∴cosα=±
| 2 |
| 3 |
| 2 |
又∵∠α为锐角,
∴cosα=
| 2 |
| 3 |
| 2 |
故选D.
点评:本题考查同角的三角函数的关系,比较简单,关键是掌握sinα2+coaα2=1.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
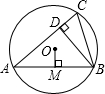 如图,已知⊙O的半径为1,锐角△ABC内接于⊙O,作BD⊥AC于点D,OM⊥AB于点M.sin∠CBD=
如图,已知⊙O的半径为1,锐角△ABC内接于⊙O,作BD⊥AC于点D,OM⊥AB于点M.sin∠CBD=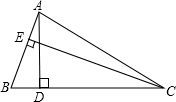 已知:如图,在△ABC中,AD⊥BC于点D,CE⊥AB于点E,BE=2AE,且
已知:如图,在△ABC中,AD⊥BC于点D,CE⊥AB于点E,BE=2AE,且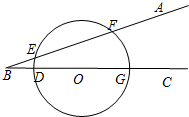 两点,EF=
两点,EF=