题目内容
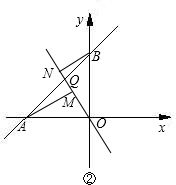
(1)如图,正△ABC中,点M与点N分别是BC、CA上的点,且BM=CN,连接AM、BN,两线交于点Q,求∠AQN的度数.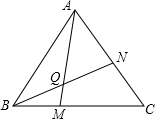
(2)将1题中的“正△ABC”分别改为正方形ABCD,正五边形ABCDE,正六边形ABCDEF,…,正n边形ABCD…N,其余条件不变,根据第1题的求解思路分别推断∠AQN的度数,将结论填入下表:
| 正多边形 | 正方形 | 正五边形 | 正六边形 | … | 正n边形 |
| ∠AQN的度数 |
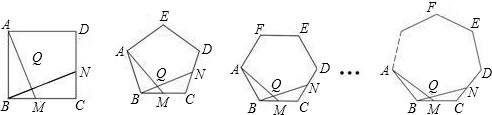
分析:(1)∠AQN即∠ABN与∠BAM之和,求解△ABM≌△BCN,∠BAM=∠CBN,进而可求解;
(2)由(1)可得,∠AQN的大小即多边形一个角的大小,所以此结论可推广到n边形.
(2)由(1)可得,∠AQN的大小即多边形一个角的大小,所以此结论可推广到n边形.
解答:解:(1)在△ABM与△BCN中,
,
∴△ABM≌△BCN(SAS),
∴∠BAM=∠NBC,
∴∠AQN=∠BAM+∠ABQ,
=∠NBC+∠ABQ,
=∠ABM=60°
∴∠AQN=60°;
(2)由(1)可知,∠AQN=各个多边形的一个角的大小,
所以正方形中∠AQN=90°,
正五边形中∠AQN=108°,
正六边形中∠AQN=120°,
…
正n边形中∠AQN=
.
|
∴△ABM≌△BCN(SAS),
∴∠BAM=∠NBC,
∴∠AQN=∠BAM+∠ABQ,
=∠NBC+∠ABQ,
=∠ABM=60°
∴∠AQN=60°;
(2)由(1)可知,∠AQN=各个多边形的一个角的大小,
所以正方形中∠AQN=90°,
正五边形中∠AQN=108°,
正六边形中∠AQN=120°,
…
正n边形中∠AQN=
| (n-2)•180° |
| n |
点评:熟练掌握等边三角形的性质及正方形,多边形的性质.

练习册系列答案
相关题目
 1、如图,正五边形FGHMN是由正五边形ABCDE经过位似变换得到的,若AB:FG=2:3,则下列结论正确的是( )
1、如图,正五边形FGHMN是由正五边形ABCDE经过位似变换得到的,若AB:FG=2:3,则下列结论正确的是( )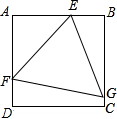 如图,正△EFG内接于正方形ABCD,其中E,F,G分别在边AB,AD,BC上,若
如图,正△EFG内接于正方形ABCD,其中E,F,G分别在边AB,AD,BC上,若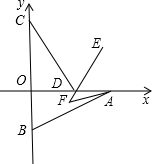 轴正半轴).
轴正半轴).