题目内容
若边长为4的菱形的两邻角度数之比为1：2，则该菱形的面积为（ ）
分析：首先过点D作DE⊥AB于点E，由两个邻角∠A与∠B的比是1：2，可求得∠A=60°，然后由三角函数，求得DE的长，继而求得这个菱形的面积．
解答：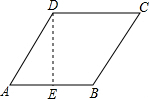
解：如图：过点D作DE⊥AB于点E．
∵菱形ABCD的两个邻角∠A与∠B的比是1：2，
∴∠A=60°，
∴AB=AD=4，
∴DE=AD•sin60°=2
，
∴这个菱形的面积为：AB•DE=4×2
=8
．
故选B．
解：如图：过点D作DE⊥AB于点E．∵菱形ABCD的两个邻角∠A与∠B的比是1：2，
∴∠A=60°，
∴AB=AD=4，
∴DE=AD•sin60°=2
| 3 |
∴这个菱形的面积为：AB•DE=4×2
| 3 |
| 3 |
故选B．
点评：此题考查了菱形的性质以及三角函数的定义．此题难度不大，注意掌握辅助线的作法，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
