题目内容
17、如图，则|a-b|-|a-c|=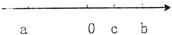
b-c
．分析：先根据数轴上的大小关系确定绝对值符号内代数式的正负情况a-b＜0，a-c＜0，再根据绝对值的性质去掉绝对值符号进行有理数运算即可求解．注意：数轴上的点右边的总比左边的大．
解答：解：根据数轴可知a＜0＜c＜b，
所以a-b＜0，a-c＜0，
则|a-b|-|a-c|=-（a-b）+（a-c）=-a+b+a-c=b-c．
所以a-b＜0，a-c＜0，
则|a-b|-|a-c|=-（a-b）+（a-c）=-a+b+a-c=b-c．
点评：此题综合考查了数轴、绝对值的有关内容，用几何方法借助数轴来求解，非常直观，且不容易遗漏，体现了数形结合的优点．要注意先确定绝对值符号内代数式的正负情况，再根据绝对值的性质去掉绝对值符号进行有理数运算．
练习册系列答案
优学名师名题系列答案
相关题目
15、抛物线y=ax2+bx+c的图象如图，则（ ）
二次函数y=ax2+bx+c的图象如图，则下列各式中成立的个数是（ ）
如图所示，镜子里号码如图，则实际纸上的号码是