题目内容
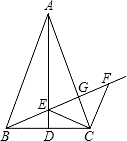如图，△ABC中，AB=AC，D为BC中点，E为AD上任意一点，过C作CF∥AB交BE的延长线于F，交AC于G，连接CE．下列结论中不正确的有（ ）| A、AD平分∠BAC | ||
| B、BE=CF | ||
| C、BE=CE | ||
D、若BE=5，GE=4，则GF=
|
分析：根据等腰三角形三线合一的特点即可判断A、C选项是正确的；关于D选项，可通过证△ECG和△EFC相似，根据相似三角形得出的对应成比例线段，来判断其结论是否正确．
解答：解：∵△ABC中，AB=AC，D为BC中点，
∴AD是线段BC的垂直平分线，
∴AD平分∠BAC，BE=CE．
故A、C正确．
∵CF∥AB，
∴∠CFG=∠ABF；
∵∠ABE=∠ACE，
∴∠CFG=∠ACE=∠CFE；
∵∠CEG=∠FEC，
∴△ECG∽△EFC；
∴EC2=EG•EF；①
当BE=5，GE=4时，由①可得：EF=
=
=
=
；
∴GF=EF-GE=
-4=
；
因此D正确．
故本题选B．
∴AD是线段BC的垂直平分线，
∴AD平分∠BAC，BE=CE．
故A、C正确．
∵CF∥AB，
∴∠CFG=∠ABF；
∵∠ABE=∠ACE，
∴∠CFG=∠ACE=∠CFE；
∵∠CEG=∠FEC，
∴△ECG∽△EFC；
∴EC2=EG•EF；①
当BE=5，GE=4时，由①可得：EF=
| EC2 |
| EG |
| BE2 |
| EG |
| 52 |
| 4 |
| 25 |
| 4 |
∴GF=EF-GE=
| 25 |
| 4 |
| 9 |
| 4 |
因此D正确．
故本题选B．
点评：本题主要考查了等腰三角形的性质、平行线的性质、相似三角形的判定和应用等知识，综合性强，难度较大．
练习册系列答案
名校课堂系列答案
相关题目
26、已知：如图，△ABC中，点D在AC的延长线上，CE是∠DCB的角平分线，且CE∥AB．
27、已知：如图，△ABC中，∠BAC=60°，D、E两点在直线BC上，连接AD、AE．
27、如图，△ABC中，AD⊥BC于D，DN⊥AC于N，DM⊥AB于M
14、如图，△ABC中，∠BAC=120°，AD⊥BC于D，且AB+BD=DC，则∠C的大小是（ ）
已知，如图，△ABC中，点D在BC上，且∠1=∠C，∠2=2∠3，∠BAC=70°．