题目内容
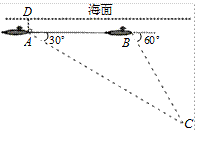
如图,一艘核潜艇在海面下500米A点处测得俯角为30°正前方的海底有黑匣子信号发出,继续在同一深度直线航行4000米后再次在B点处测得俯角为60°正前方的海底有黑匣子信号发出,求海底黑匣子C点处距离海面的深度?(精确到米,参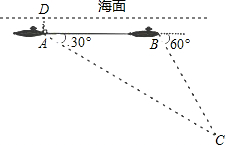 考数据:
考数据:| 2 |
| 3 |
| 5 |
分析:易证∠BAC=∠BCA,所以有BA=BC.然后在直角△BCE中,利用正弦函数求出CE.
解答: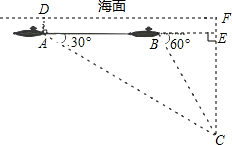 解:由C点向AB作垂线,交AB的延长线于E点,并交海面于F点.
解:由C点向AB作垂线,交AB的延长线于E点,并交海面于F点.
已知AB=4000(米),∠BAC=30°,∠EBC=60°,
∵∠BCA=∠EBC-∠BAC=30°,
∴∠BAC=∠BCA.
∴BC=BA=4000(米).
在Rt△BEC中,
EC=BC•sin60°=4000×
=2000
(米).
∴CF=CE+EF=2000
+500≈3964(米).
答:海底黑匣子C点处距离海面的深度约为3964米.
 解:由C点向AB作垂线,交AB的延长线于E点,并交海面于F点.
解:由C点向AB作垂线,交AB的延长线于E点,并交海面于F点.已知AB=4000(米),∠BAC=30°,∠EBC=60°,
∵∠BCA=∠EBC-∠BAC=30°,
∴∠BAC=∠BCA.
∴BC=BA=4000(米).
在Rt△BEC中,
EC=BC•sin60°=4000×
| ||
| 2 |
| 3 |
∴CF=CE+EF=2000
| 3 |
答:海底黑匣子C点处距离海面的深度约为3964米.
点评:本题要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
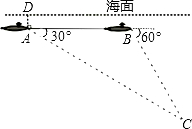
 如图,一艘核潜艇在海面下400米的A处测得俯角为30°的海底有黑匣子C信号发出,在同一深度继续直线航行1000米的B处测得俯角为45°的正前方海底有黑匣子C的信号发出,求海底黑匣子C距离海面的深度.
如图,一艘核潜艇在海面下400米的A处测得俯角为30°的海底有黑匣子C信号发出,在同一深度继续直线航行1000米的B处测得俯角为45°的正前方海底有黑匣子C的信号发出,求海底黑匣子C距离海面的深度. 如图,一艘核潜艇在海面下700米A处测得俯角为30°正前方的海底C处有黑匣子信号发出,继续在同一深度直线航行8000米后在B处测得俯角为60°正前方的海底C处有黑匣子信号发出.点C和直线AB在同一铅垂面上,求点C距离海面的深度.(结果保留整数,参考数据
如图,一艘核潜艇在海面下700米A处测得俯角为30°正前方的海底C处有黑匣子信号发出,继续在同一深度直线航行8000米后在B处测得俯角为60°正前方的海底C处有黑匣子信号发出.点C和直线AB在同一铅垂面上,求点C距离海面的深度.(结果保留整数,参考数据