题目内容
 已知点E在矩形ABCD边CD上,将矩形沿AE折叠后点D落在点D′,∠CED′=35°,则∠BAD′的大小是
已知点E在矩形ABCD边CD上,将矩形沿AE折叠后点D落在点D′,∠CED′=35°,则∠BAD′的大小是
- A.40°
- B.45°
- C.55°
- D.60°
C
分析:先根据图形翻折变换的性质得出∠D=∠D′=90°,再由∠CED′=35°即可求出∠DED′的度数,再由四边形内角和定理求出∠DAD′的度数,根据∠BAD′=∠DAB-DAD′即可得出结论.
解答: 解:∵△AD′E由△ADE翻折而成,
解:∵△AD′E由△ADE翻折而成,
∠D=∠D′=90°,
∵∠CED′=35°,
∴∠DED′=180°-∠CED′=180°-35°=145°,
∴∠DAD′=180°-∠DED′=180°-145°=35°,
∴∠BAD′=∠DAB-DAD′=90°-35°=55°.
故选C.
点评:本题考查的是翻折变换,熟知折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解答此题的关键.
分析:先根据图形翻折变换的性质得出∠D=∠D′=90°,再由∠CED′=35°即可求出∠DED′的度数,再由四边形内角和定理求出∠DAD′的度数,根据∠BAD′=∠DAB-DAD′即可得出结论.
解答:
 解:∵△AD′E由△ADE翻折而成,
解:∵△AD′E由△ADE翻折而成,∠D=∠D′=90°,
∵∠CED′=35°,
∴∠DED′=180°-∠CED′=180°-35°=145°,
∴∠DAD′=180°-∠DED′=180°-145°=35°,
∴∠BAD′=∠DAB-DAD′=90°-35°=55°.
故选C.
点评:本题考查的是翻折变换,熟知折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解答此题的关键.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
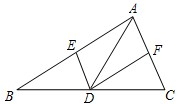 22、如图,已知点D在△ABC的BC边上,DE∥AC交AB于E,DF∥AB交AC于F.
22、如图,已知点D在△ABC的BC边上,DE∥AC交AB于E,DF∥AB交AC于F.

