题目内容
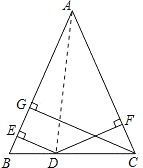
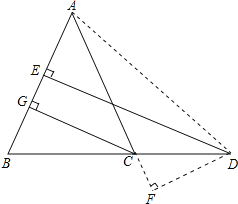
【题目】如图，在△ABC中，AB=AC，D是BC上任意一点，过D分别向AB，AC引垂线，垂足分别为E，F，CG是AB边上的高．
（1）当D点在BC的什么位置时，DE=DF？请说明理由．
（2）DE，DF，CG的长之间存在着怎样的等量关系？并说明理由.
（3）若D在底边BC的延长线上，（2）中的结论还成立吗？若不成立，又存在怎样的关系？并说明理由.
【答案】（1）当点D在BC的中点时，DE=DF，理由见解析；（2）DE+DF=CG．理由见解析；（3）当点D在BC延长线上时，（2）中的结论不成立，但有DE﹣DF=CG．理由见解析.
【解析】分析：（1）当点D在BC的中点时，DE=DF，根据AAS证△BED≌△CFD，根据全等三角形的性质推出即可；
（2）连接AD，根据三角形ABC的面积=三角形ABD的面积+三角形ACD的面积，进行分析证明；
（3）类似（2）的思路，仍然用计算面积的方法来确定线段之间的关系．即三角形ABC的面积=三角形ABD的面积-三角形ACD的面积．
详解：（1）当点D在BC的中点时，DE=DF，理由如下：
∵D为BC中点，∴BD=CD，
∵AB=AC，∴∠B=∠C，
∵DE⊥AB，DF⊥AC，∴∠DEB=∠DFC=90°，
在△BED和△CFD中
∠B=∠C，∠DEB=∠DFC，BD=CD，
∴△BED≌△CFD（AAS），∴DE=DF．
（2）DE+DF=CG．
理由：连接AD，
则S△ABC=S△ABD+S△ACD，即
ABCG=ABDE+ACDF，
∵AB=AC，∴CG=DE+DF．
（3）当点D在BC延长线上时，（2）中的结论不成立，但有DE﹣DF=CG．
理由：连接AD，则S△ABD=S△ABC+S△ACD，即ABDE=ABCG+ACDF
∵AB=AC，∴DE=CG+DF，即DE﹣DF=CG．
同理当D点在CB的延长线上时，（2）中结论不成立，则有DE﹣DF=CG，说明方法同上．
