题目内容
如图，已知正方形ABCD和CEFG，连接DE，以DE为边作正方形EDHI，试用该图形证明勾股定理：CD2+CE2=DE2．
练习册系列答案
口算题天天练系列答案
相关题目
如图，在平面直角坐标系中，反比例函数y1=| 2 |
| x |
| A、1＜x＜3 |
| B、x＜0或1＜x＜3 |
| C、0＜x＜1 |
| D、x＞3或0＜x＜1 |
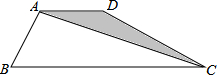如图，四边形ABCD中，AB=AD，AD∥BC，∠ABC=60°，∠BCD=30°，BC=6，那么△ACD的面积是（ ）A、
| ||||
B、
| ||||
C、2
| ||||
D、
|
我国汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图”，后人称其为“赵爽弦图”（如图1），图2由弦图变化得到，它是由作个全等的直角三角形拼接而成，记图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为S1、S2、S3，若S1+S2+S3=10，则S2的值是（ ）
| A、5 | ||
B、
| ||
C、
| ||
| D、4 |
2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽弦图它是由四全等的直角三角形与中间的一个小正方形拼成的一个大正方形，如图所示，如果大正方形 的面积是13，小正方形的面积是1，直角三角形的短直角边为a，较长直角边为b，下列说法：
如图，△ABC中，∠C=45°，点D在AB上，点E在BC上．若AD=DB=DE，AE=1，则AC的长为（ ）分别以下列四组数为一个三角形的三边长：①6，8，10；②13，5，12 ③1，2，3；④9，40，41；其中能构成直角三角形的有（ ）
| A、1组 | B、2组 | C、3组 | D、4组 |
如图，△ABC的周长为16，G、H分别为AB、AC的中点，分别以AB、AC为斜边向外作Rt△ADB和Rt△AEC，连接DG、GH、EH，则DG+GH+EH的值为（ ）在四边形ABCD中，对角线AC、BD相交于点O，∠ADB=∠CBD，添加下列一个条件后，仍不能判定四边形ABCD是平行四边形的是（ ）
| A、∠ABD=∠CDB | B、∠DAB=∠BCD | C、∠ABC=∠CDA | D、∠DAC=∠BCA |