题目内容
求作一个平行四边形,使其两邻边分别为a和2a,且两条对角线所成的锐角为60°.这样的平行四边形应当是( )
| A.仅有一个 | B.有两个 | C.有无穷多个 | D.一个也没有 |
如图
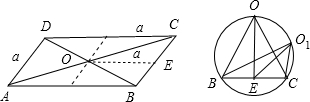
直观得出,以BC=a为底边、顶角0为60°的所有△OBC中点O的轨迹为不含B、C两点的优弧
(如图乙),
其中,底边BC上中线的最大值为正△OBC的高OE,
而OE=
a<a,这与图(甲)中平行四边形中OE=a矛盾,
故这样的平行四边形不存在.
故选D.

直观得出,以BC=a为底边、顶角0为60°的所有△OBC中点O的轨迹为不含B、C两点的优弧
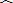 |
| BC |
其中,底边BC上中线的最大值为正△OBC的高OE,
而OE=
| ||
| 2 |
故这样的平行四边形不存在.
故选D.

练习册系列答案
相关题目
求作一个平行四边形,使其两邻边分别为a和2a,且两条对角线所成的锐角为60°.这样的平行四边形应当是( )
| A、仅有一个 | B、有两个 | C、有无穷多个 | D、一个也没有 |