题目内容
【题目】边长为6的等边△ABC中，点P从点A出发沿射线AB方向移动，同时点Q从点B出发，以相同的速度沿射线BC方向移动，连接AQ、CP，直线AQ、CP相交于点D．
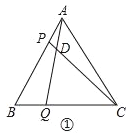
（1）如图①，当点P、Q分别在边AB、BC上时，
①连接PQ，当△BPQ是直角三角形时，AP等于_____；
②∠CDQ的大小是否随P，Q的运动而变化？如果不会，请求出∠CDQ的度数；如果会，请说明理由；
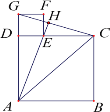
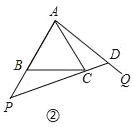
（2）当P、Q分别在边AB、BC的延长线上时，在图②中画出点D，并直接写出∠CDQ的度数．
【答案】（1）①2或4；②60°；（2）120°.
【解析】分析：
（1）①如图3，由题意可知∠B=60°，然后分∠PQB=90°和∠QPB=90°两种情况结合已知条件进行解答即可；②由已知条件易证△ABQ≌△CAP，由此可得∠BAQ=∠ACP，从而可得∠CDQ=∠DAC+∠ACP=∠DAC+∠BAQ=∠CAB=60°，由此可得∠CDQ的大小不随点P、Q的运动而改变；
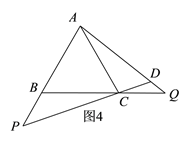
（2）如图4，由题意易证△ABQ≌△CAP，从而可得∠Q=∠P，结合∠P+∠BCP=60°可得∠Q+∠DCQ=60°，从而可得此时∠CDQ=120°．
详解：
（1）如图3，连接PQ，
①∵△ABC是等边三角形，
∴∠B=60°，
由题意得，AP=BQ，
当∠PQB=90°时，BQ=
BP，即AP=（6﹣AP）
解得，AP=2，
当∠QPB=90°时，BQ=2BP，即AP=2（6﹣AP）
解得，AP=4，
综上所述，当AP=2或4时，△BPQ是直角三角形，
故答案为：2或4；
②∠CDQ的大小不变
∵P、Q用时出发，速度相同，所以AP=BQ，
∵△ABC是等边三角形，
∴BA=AC，∠B=∠CAP=60°，
在△ABQ和△CAP中，
BA=AC，∠B=∠APC，BQ=AP，
∴△ABQ≌△CAP，
∴∠BAQ=∠ACP，
∴∠CDQ=∠DAC+∠ACP=∠DAC+∠BAQ=∠CAB=60°；
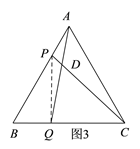
（2）如图4，∠CDQ=120°，理由如下：
∵△ABC是等边三角形，
∴BA=AC，∠ABC=∠CAP=60°，
在△ABQ和△CAP中，
BA=AC，∠ABQ=∠CAP，BQ=AP，
∴△ABQ≌△CAP，
∴∠Q=∠P，
∵∠P+∠BCP=60°，
∴∠Q+∠DCQ=60°，
∴∠CDQ=120°．
