题目内容
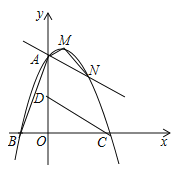
【题目】如图,在直角坐标系中有![]() ,
,![]() 为坐标原点,
为坐标原点,![]() ,将此三角形绕原点
,将此三角形绕原点![]() 顺时针旋转
顺时针旋转![]() ,得到
,得到![]() ,二次函数
,二次函数![]() 的图象刚好经过
的图象刚好经过![]() 三点.
三点.
(1)求二次函数的解析式及顶点![]() 的坐标;
的坐标;
(2)过定点![]() 的直线
的直线![]() 与二次函数图象相交于
与二次函数图象相交于![]() 两点.
两点.
①若![]() ,求
,求![]() 的值;
的值;
②证明:无论![]() 为何值,
为何值,![]() 恒为直角三角形;
恒为直角三角形;
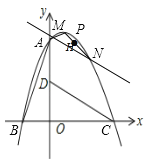
③当直线![]() 绕着定点
绕着定点![]() 旋转时,
旋转时,![]() 外接圆圆心在一条抛物线上运动,直接写出该抛物线的表达式.
外接圆圆心在一条抛物线上运动,直接写出该抛物线的表达式.
【答案】(1)![]() ,
,![]() ;(2)①
;(2)①![]() ;②见解析;③
;②见解析;③![]() .
.
【解析】
(1)求出点A、B、C的坐标分别为(0,3)、(-1,0)、(3,0),即可求解;
(2)①S△PMN=![]() PQ×(x2-x1),则x2-x1=4,即可求解;②k1k2=
PQ×(x2-x1),则x2-x1=4,即可求解;②k1k2=![]() =-1,即可求解;③取MN的中点H,则点H是△PMN外接圆圆心,即可求解.
=-1,即可求解;③取MN的中点H,则点H是△PMN外接圆圆心,即可求解.
(1)![]() ,则
,则![]() ,
,
即点![]() 的坐标分别为
的坐标分别为![]() 、
、![]() 、
、![]() ,
,
则二次函数表达式为:![]() ,
,
即:![]() ,解得:
,解得:![]() ,
,
故函数表达式为:![]() ,
,
点![]() ;
;
(2)将二次函数与直线![]() 的表达式联立并整理得:
的表达式联立并整理得:
![]() ,
,
设点![]() 的坐标为
的坐标为![]() 、
、![]() ,
,
则![]() ,
,
则:![]() ,
,
同理:![]() ,
,
①![]() ,当
,当![]() 时,
时,![]() ,即点
,即点![]() ,
,
![]() ,则
,则![]() ,
,
![]() ,
,
解得:![]() ;
;
②点![]() 的坐标为
的坐标为![]() 、
、![]() 、点
、点![]() ,
,
则直线![]() 表达式中的
表达式中的![]() 值为:
值为:![]() ,直线
,直线![]() 表达式中的
表达式中的![]() 值为:
值为:![]() ,
,
为: ![]() ,
,
故![]() ,
,
即:![]() 恒为直角三角形;
恒为直角三角形;
③取![]() 的中点
的中点![]() ,则点
,则点![]() 是
是![]() 外接圆圆心,
外接圆圆心,
设点![]() 坐标为
坐标为![]() ,
,
则![]() ,
,
![]() ,
,
整理得:![]() ,
,
即:该抛物线的表达式为:![]() .
.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目