题目内容
PA,PB,CD是⊙O的切线,A,B,E是切点,CD分别交PA,PB于C,D两点,若∠APB=40°,则∠COD的度数是( )
| A.50° | B.60° | C.70° | D.75° |
C.
试题分析:画出图形如图:
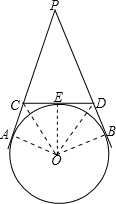
连接OA、OC、OE、OD、OB,所得图形如下:
由切线性质得,OA⊥PA,OB⊥PB,OE⊥CD,DB=DE,AC=CE,
∵AO=OE=OB,
∴△AOC≌△EOC(SAS),△EOD≌△BOD(SAS),
∴∠AOC=∠EOC,∠EOD=∠BOD,
∴∠COD=
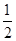 ∠AOB,
∠AOB,∵∠APB=40°,
∴∠AOB=140°,
∴∠COD=70°.
故选C.
考点: 切线的性质.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
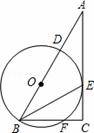
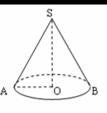
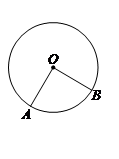
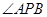 =
=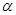 ,∠AQB=
,∠AQB=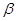 ,则
,则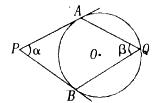
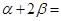 90° B.
90° B. 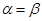 C.
C. 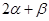 =180° D.
=180° D.