题目内容
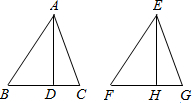 如图,AD,EH分别是锐角△ABC和锐角△EFG的高,且AB=EF,AD=EH.若使△ABC≌△EFG,需补充一个条件
如图,AD,EH分别是锐角△ABC和锐角△EFG的高,且AB=EF,AD=EH.若使△ABC≌△EFG,需补充一个条件BC=FG或∠BAC=∠FEG或∠C=∠G
BC=FG或∠BAC=∠FEG或∠C=∠G
(填写一个你认为适当的条件即可).分析:根据“HL”可以判定△ABD和△EFH全等,根据全等三角形对应角相等可得∠B=∠F,然后根据利用全等三角形的不同的判定方法可以补充不同的条件.
解答:解:∵AD,EH分别是锐角△ABC和锐角△EFG的高,
∴△ABD、△EFH都是直角三角形,
在Rt△ABD和Rt△EFH中,
∵
,
∴Rt△ABD≌Rt△EFH(HL),
∴∠B=∠F,
①补充的条件为BC=FG,则根据“边角边”可得△ABC≌△EFG;
②补充的条件为∠BAC=∠FEG,则根据“角边角”可得△ABC≌△EFG;
③补充的条件为∠C=∠G,则根据“角角边”可得△ABC≌△EFG.
所以可补充的条件为BC=FG或∠BAC=∠FEG或∠C=∠G.
故答案为:BC=FG或∠BAC=∠FEG或∠C=∠G.
∴△ABD、△EFH都是直角三角形,
在Rt△ABD和Rt△EFH中,
∵
|
∴Rt△ABD≌Rt△EFH(HL),
∴∠B=∠F,
①补充的条件为BC=FG,则根据“边角边”可得△ABC≌△EFG;
②补充的条件为∠BAC=∠FEG,则根据“角边角”可得△ABC≌△EFG;
③补充的条件为∠C=∠G,则根据“角角边”可得△ABC≌△EFG.
所以可补充的条件为BC=FG或∠BAC=∠FEG或∠C=∠G.
故答案为:BC=FG或∠BAC=∠FEG或∠C=∠G.
点评:本题考查了全等三角形的判定,根据不同的判定方法,可以补充的条件也不相同,熟记各判定方法是解题的关键.

练习册系列答案
相关题目
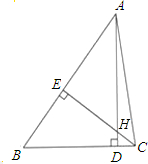 如图,在△ABC中AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知EH=EB=3,AE=4,则BC+AC的长是( )
如图,在△ABC中AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知EH=EB=3,AE=4,则BC+AC的长是( )| A、7 | ||
| B、8 | ||
C、5+4
| ||
D、9
|
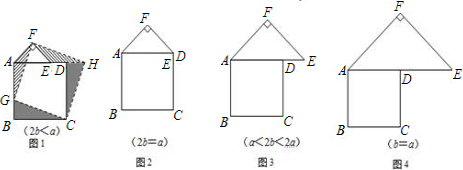

 na=
na=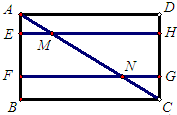 如图,在矩形ABCD中,EH∥FG∥AD,EH,FG分别交AC于点M,N,EF=
如图,在矩形ABCD中,EH∥FG∥AD,EH,FG分别交AC于点M,N,EF= 如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知EH=EB=3,AE=4,则CH的长是
如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知EH=EB=3,AE=4,则CH的长是