题目内容
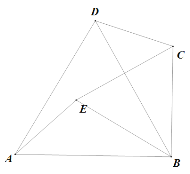
【题目】如图:两个等边三角形△ABD与△BCE,连结AE与CD,
求证:(1)AE=CD;
(2)AE与DC之间的夹角为60°;
(3)AE与CD的交点设为H,BH平分∠AHC.
【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】
(1)根据等边三角形的性质,易证△BCD≌△BEA,即可证得AE=CD;
(2)延长AE交CD于H,交BD于O,在△ODH和△AOB中,根据“8” 字形即可证明;
(3)过B作BM⊥CD于点M,过B作BN⊥AH于点N,证明△AMN≌△DBM,得出 BM=BN,即可通过角平分线的判定证明.
(1)∵等边三角形ABD和等边三角形BCE
∴∠ABD=∠CBE=60°,AB=BD,BE=BC,∠ABD-∠EBD=∠CBE-∠EBD,即∠ABE=∠DBC,
∴△BCD≌△BEA,
∴AE=DC
(2)延长AE交CD于H,交BD于O,在△ODH和△AOB中,
∵△BCD≌△BEA,
∴∠HDO=∠OAB,
又∵∠DOH=∠AOB,根据三角形内角和是180°,
∴∠DHO=∠ABO=60°

(3)过B作BM⊥CD交CD的延长线于点M,过B作BN⊥AH于点N,
∴∠BNA=∠BMD=90°,
∵△BCD≌△BEA,
∴AB=DB, ∠BAN=∠BDM
∴△AMN≌△DBM
∴BM=BN,
∴BH平分∠AHC.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目