题目内容
【题目】如图,在![]() 中,
中, ![]() 是
是![]() 的轴对称图形,点E在AD上,点F在AC的延长线上
的轴对称图形,点E在AD上,点F在AC的延长线上![]() 若点B恰好在EF的垂直平分线上,并且
若点B恰好在EF的垂直平分线上,并且![]() ,
,![]() ,则
,则![]() ______.
______.

【答案】4.
【解析】
连接BE,BF,根据轴对称的性质可得△ABD≌△ACB,进而可得DB=CB,AD=AC,∠D=∠BCA=90°,再利用线段垂直平分线的性质可得BE=BF,然后证明Rt△DBE≌Rt△CBF可得DE=CF,然后可得ED长.
解:连接BE,BF,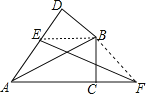
∵△ABD是△ABC的轴对称图形,
∴△ABD≌△ACB,
∴DB=CB,AD=AC,∠D=∠BCA=90°,
∴∠BCF=90°,
∵点B恰好在EF的垂直平分线上,
∴BE=BF,
在Rt△DBE和Rt△CBF中
![]() ,
,
∴Rt△DBE≌Rt△CBF(HL),
∴DE=CF,
设DE=x,则CF=x,
∵AE=5,AF=13,
∴AC=AD=5+x,
∴AF=5+2x,
∴5+2x=13,
∴x=4,
∴DE=4,
故答案为:4.

练习册系列答案
相关题目