题目内容
在△ABC中,已知∠C=90°,sinB= ,则cosA的值是
,则cosA的值是
- A.

- B.

- C.

- D.

D
分析:利用三角函数的定义,定义成三角形的边的比值,即可求解.
解答: 解:在直角△ABC中设∠C=90°.
解:在直角△ABC中设∠C=90°.
∵sinB=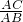 =
= ,
,
设AC=3x,则AB=5x,
根据勾股定理可得:BC=4x.
∴cosA=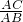 =
=
故选D.
点评:本题主要考查了三角函数的定义,求锐角的三角函数值的方法:利用锐角三角函数的定义,通过设参数的方法求三角函数值,或者利用同角(或余角)的三角函数关系式求三角函数值.
分析:利用三角函数的定义,定义成三角形的边的比值,即可求解.
解答:
 解:在直角△ABC中设∠C=90°.
解:在直角△ABC中设∠C=90°.∵sinB=
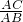 =
= ,
,设AC=3x,则AB=5x,
根据勾股定理可得:BC=4x.
∴cosA=
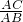 =
=
故选D.
点评:本题主要考查了三角函数的定义,求锐角的三角函数值的方法:利用锐角三角函数的定义,通过设参数的方法求三角函数值,或者利用同角(或余角)的三角函数关系式求三角函数值.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目