题目内容
问题:在△ABC中,AB、BC、AC三边的长分别为
、
、
,求这个三角形的面积.
小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图所示,这样不需求△ABC的高,而借用网格就能计算出它的面积.
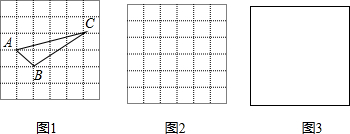
(1)请你将△ABC的面积直接填写在横线上
.
(2)我们把上述求△ABC面积的方法叫做构图法.若△ABC三边的长分别为
a、2
a、
a(a>0),请利用图2的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积是:
(3)若△ABC三边的长分别为
、
、2
(m>0,n>0,m≠n),请运用构图法在图3指定区域内画出示意图,并求出△ABC的面积为:
| 2 |
| 13 |
| 17 |
小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图所示,这样不需求△ABC的高,而借用网格就能计算出它的面积.

(1)请你将△ABC的面积直接填写在横线上
| 5 |
| 2 |
| 5 |
| 2 |
(2)我们把上述求△ABC面积的方法叫做构图法.若△ABC三边的长分别为
| 2 |
| 5 |
| 26 |
3a2
3a2
.(3)若△ABC三边的长分别为
| 4m2+n2 |
| 16m2+n2 |
| m2+n2 |
4mn
4mn
.分析:(1)利用恰好能覆盖△ABC的长为4,宽为2的小矩形的面积减去三个小直角三角形的面积即可解答;
(2)
a是直角边为a的等腰直角三角形的斜边,2
a是直角边长为4a,2a的直角三角形的斜边;
a是直角边长为5a,a的直角三角形的斜边;,把它整理为一个矩形的面积减去三个直角三角形的面积;
(3)结合(1),(2)易得此三角形的三边分别是直角边长为2m,n的直角三角形的斜边;直角边长为4m,n的直角三角形的斜边;直角边长为2m,2n的直角三角形的斜边.同样把它整理为一个矩形的面积减去三个直角三角形的面积.
(2)
| 2 |
| 5 |
| 26 |
(3)结合(1),(2)易得此三角形的三边分别是直角边长为2m,n的直角三角形的斜边;直角边长为4m,n的直角三角形的斜边;直角边长为2m,2n的直角三角形的斜边.同样把它整理为一个矩形的面积减去三个直角三角形的面积.
解答: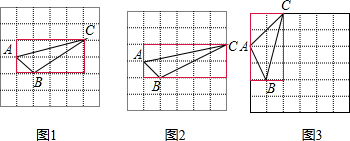 解:(1)如图1,S△ABC=2×4-
解:(1)如图1,S△ABC=2×4-
×1×1-
×1×4-
×2×3=
;
故填:
;
(2)如图2,S△ABC=2a×5a-
×a×a-
×2a×4a-
×5a×a=3a2;
故填:3a2;
(3)如图3,S△ABC=2n×4m-
×2m×n-
×4m×n-
×2m×2n=4mn;
故填:4mn.
 解:(1)如图1,S△ABC=2×4-
解:(1)如图1,S△ABC=2×4-| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
故填:
| 5 |
| 2 |
(2)如图2,S△ABC=2a×5a-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故填:3a2;
(3)如图3,S△ABC=2n×4m-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故填:4mn.
点评:本题是开放性的探索问题,关键是结合网格用矩形及容易求得面积的直角三角形表示出所求三角形的面积进行解答.

练习册系列答案
相关题目
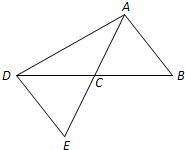 23、如图,A、B两点分别位于一池塘两侧,池塘左边有一水房D,在DB中点C处有一棵百年古槐,小明从A点出发,沿AC一直向前走到点E(A、C、E三点在同一条直线上),并使CE=CA,然后他测量出点E到水房D的距离,则DE的长度就是A、B两点间的距离.
23、如图,A、B两点分别位于一池塘两侧,池塘左边有一水房D,在DB中点C处有一棵百年古槐,小明从A点出发,沿AC一直向前走到点E(A、C、E三点在同一条直线上),并使CE=CA,然后他测量出点E到水房D的距离,则DE的长度就是A、B两点间的距离.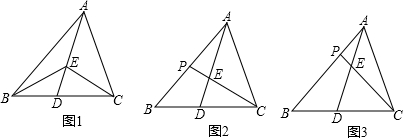
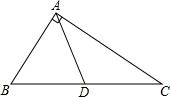 (1)如图,在△ABC中,AD是BC边上的中线,且AD=
(1)如图,在△ABC中,AD是BC边上的中线,且AD=