Question

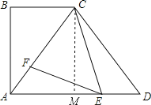
【题目】如图，在四边形ABCD中，AD∥BC，∠B＝90°，AB＝8，tan∠CAD＝，CA＝CD，E、F分别是AD、AC上的动点（点E与A、D不重合），且∠FEC＝∠ACB．

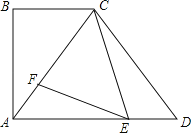
（1）求CD的长；

（2）若AF＝2，求DE的长．

Answer 1

【答案】（1）CD＝10；（2）DE＝2或10．

【解析】

（1）由AD∥BC，可得∠CAD的正弦值，在直角三角形ACB中可求得到AC，从而求得CD的长度；

（2）作CM⊥AD于点M．利用两角对应相等求得三角形AEF与三角形DCE相似，利用其性质可求DE的长．

（1）∵AD∥BC，

∴∠CAD＝∠ACB，

又∵∠B＝90°，tan∠CAD＝，AB＝8，

∴BC＝6，，

∴AC＝10，

∴CD＝CA＝10；

（2）作CM⊥AD于点M．

∵AC＝10，，

∴CM＝8，

∴AM＝6，

∴AD＝2AM＝12，

∵CA＝CD，

∴∠CAD＝∠CDA，

又∵∠FEC＝∠ACB＝∠CAD，

∴∠AFE＝∠DEC，

∴△AEF∽△DCE，

∴ ，

又∵AF＝2，BC＝6，CD＝10，AD＝12，

设x＝DE，得，

整理解得x＝2或x＝10，

即DE＝2或DE＝10．