题目内容
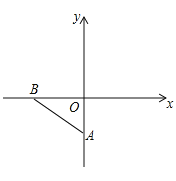
【题目】如图,在平面直角坐标系中,点B,A分别在x轴、y轴上,![]() ,在坐标轴上找一点C,使得
,在坐标轴上找一点C,使得![]() 是等腰三角形,则符合条件的等腰三角形ABC有________个.
是等腰三角形,则符合条件的等腰三角形ABC有________个.
【答案】6
【解析】
根据等腰三角形的定义、圆的性质(同圆的半径相等)分情况讨论即可得.
设点A坐标为![]() ,则
,则![]()
![]()
![]()
![]()
依题意,有以下三种情况:
(1)当![]() 时,
时,![]() 是等腰三角形
是等腰三角形
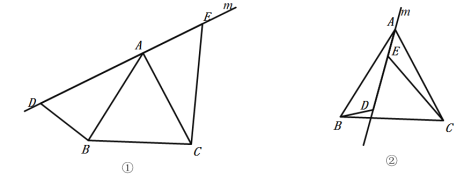
如图1,以点B为圆心、BA为半径画圆,除点A外,与坐标轴有三个交点![]()
由圆的性质可知,![]() 三点均满足要求,且
三点均满足要求,且![]() 是等边三角形
是等边三角形
![]()
![]()
(2)当![]() 时,
时,![]() 是等腰三角形
是等腰三角形
如图2,以点A为圆心、AB为半径画圆,除点B外,与坐标轴有三个交点![]()
由圆的性质可知,![]() 三点均满足要求,且
三点均满足要求,且![]() 是等边三角形
是等边三角形
![]()
![]()
(3)当![]() 时,
时,![]() 是等腰三角形
是等腰三角形
如图3,作![]() 的角平分线,交x轴于点
的角平分线,交x轴于点![]()
则![]()
![]() ,
,![]() 是等腰三角形,即点
是等腰三角形,即点![]() 满足要求
满足要求
由勾股定理得![]() ,则点
,则点![]() 坐标为
坐标为![]()
作![]() ,交y轴于点
,交y轴于点![]()
则![]() ,
,![]() 是等边三角形,即点
是等边三角形,即点![]() 满足要求
满足要求
![]()
![]() 坐标为
坐标为![]()
综上,符合条件的点共有6个:![]() (其中
(其中![]() 为同一点)
为同一点)
即符合条件的等腰三角形![]() 有6个
有6个
故答案为:6.



练习册系列答案
相关题目
【题目】甲、乙两名队员的10次射击训练,成绩分别被制成下列两个统计图.
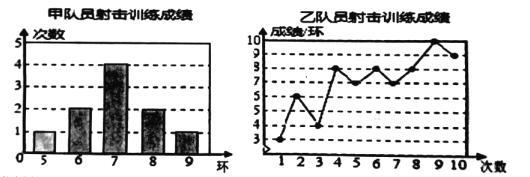
并整理分析数据如下表:
平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
甲 |
| 7 | 7 | 1.2 |
乙 | 7 |
| 8 |
|
(1)求![]() ,
,![]() ,
,![]() 的值;
的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?