题目内容
【题目】已知:直线AD,BC被直线CD所截,AC为 ∠BAD的角平分线,∠1+∠BCD=180°.
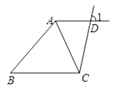
求证:∠BCA=∠BAC.
【答案】证明见解析.
【解析】分析:方法1由∠5=∠BCD可证AD∥BC,再利用角平分线的定义即可求出结果;方法2由∠ADC+∠BCD=180°可证AD∥BC,再利用角平分线的定义即可求出结果.
本题解析:
证明:
方法1 ∵ AD是一条直线,
∴∠1+∠5=180° (平角的定义)或(邻补角的定义)
∵ ∠1+∠BCD=180°(已知)
∴ ∠5=∠BCD(同角的补角相等)
∴ AD∥BC(同位角相等,两直线平行)

∴ ∠4=∠3(两直线平行,内错角相等)
∵ AC为∠BAD的角平分线(已知)
∴ ∠2=∠4(角平分线的定义)
∴ ∠2=∠3(等量代换)即:∠BCA=∠BAC.
方法2 ∵ AD与CD交于点D,
∴ ∠1=∠ADC (对顶角相等)
∵ ∠1+∠BCD=180°(已知)
∴ ∠ADC+∠BCD=180°(等量代换)
∴ AD∥BC(同旁内角互补,两直线平行)
∴ ∠4=∠3(两直线平行,内错角相等)
∵AC为∠BAD的角平分线(已知)
∴ ∠2=∠4(角平分线的定义)
∴ ∠2=∠3(等量代换)

练习册系列答案
相关题目
