题目内容
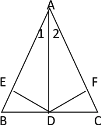
【题目】如图,A,E,F,C在一条直线上,AE=CF,过E,F分别作DE⊥AC,BF⊥AC,若AB=CD,试证明BD平分EF.

【答案】详见解析.
【解析】
根据已知条件证明AB=CD,AF=CF,证明 Rt△ABF≌Rt△CDE(HL),得BF=DE,进而证明△BFG≌△DEG(AAS),即可证明.
证明∵DE⊥AC,BF⊥AC,
∴∠DEG=∠BFE=90°,
∵AE=CF,AE+EF=CF+EF,即AF=CE.
在Rt△ABF和Rt△CDE中,AB=CD,AF=CF,
∴Rt△ABF≌Rt△CDE(HL),
∴BF=DE.
在△BFG和△DEG中,∠BFG=∠DEG,∠BGF=∠DGE,BF=DE
∴△BFG≌△DEG(AAS),
∴FG=EG,即BD平分EF

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
【题目】探究函数y=x+![]() (x>0)与y=x+
(x>0)与y=x+![]() (x>0,a>0)的相关性质.
(x>0,a>0)的相关性质.
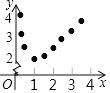
(1)小聪同学对函数y=x+![]() (x>0)进行了如下列表、描点,请你帮他完成连线的步骤;观察图象可得它的最小值为 ,它的另一条性质为 ;
(x>0)进行了如下列表、描点,请你帮他完成连线的步骤;观察图象可得它的最小值为 ,它的另一条性质为 ;
x | … |
|
|
| 1 |
| 2 |
| 3 | … |
y | … |
|
|
| 2 |
|
|
|
| … |
(2)请用配方法求函数y=x+![]() (x>0)的最小值;
(x>0)的最小值;
(3)猜想函数y=x+![]() (x>0,a>0)的最小值为 .
(x>0,a>0)的最小值为 .