题目内容
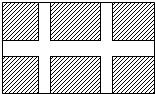
如图,八一广场要设计一个矩形花坛,花坛的长、宽分别为200m、120m,花坛中有一横两纵的通道,横、纵通道的宽度分别为3xm、2xm.(1)用代数式表示三条通道的总面积S;当通道总面积为花坛总面积的
| 11 | 125 |
(2)如果花坛绿化造价为每平方米3元,通道总造价为3168x元,那么横、纵通道的宽分别为
 多少米时,花坛总造价最低?并求出最低造价.
多少米时,花坛总造价最低?并求出最低造价.(以下数据可供参考:852=7225,862=7396,872=7569)
分析:(1)根据等量关系“三条道路的总面积=横通道的面积+纵通道的面积-重叠的面积”列出方程求解;
(2)根据等量关系“花坛总造价=绿化造价+通道造价”列出函数关系,并求得函数的最大值.
(2)根据等量关系“花坛总造价=绿化造价+通道造价”列出函数关系,并求得函数的最大值.
解答:解:(1)由题意得:
S=3x•200+2x•120×2-2×6x2=-12x2+1080x
由S=
×200×120,得:
∴-12x2+1080x=
×200×120,
即x2-90x+176=0,解得:
x=2或x=88
又∵x>0,4x<200,3x<120,
∴解得0<x<40,
∴x=2,得横、纵通道的宽分别是6m、4m.
(2)设花坛总造价为y元.
则y=3168x+(200×120-S)×3=3168x+(24000+12x2-1080x)×3
=36x2-72x+72000=36(x-1)2+71964,
当x=1,即横、纵通道的宽分别为3m、2m时,花坛总造价最低,最低总造价为71964元.
S=3x•200+2x•120×2-2×6x2=-12x2+1080x
由S=
| 11 |
| 125 |
∴-12x2+1080x=
| 11 |
| 125 |
即x2-90x+176=0,解得:
x=2或x=88
又∵x>0,4x<200,3x<120,
∴解得0<x<40,
∴x=2,得横、纵通道的宽分别是6m、4m.
(2)设花坛总造价为y元.
则y=3168x+(200×120-S)×3=3168x+(24000+12x2-1080x)×3
=36x2-72x+72000=36(x-1)2+71964,
当x=1,即横、纵通道的宽分别为3m、2m时,花坛总造价最低,最低总造价为71964元.
点评:本题考查了运用函数方程解决实际问题,并考查了函数最大值的求解问题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
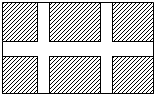 如图,八一广场要设计一个矩形花坛,花坛的长、宽分别为200m、120m,花坛中有一横两纵的通道,横、纵通道的宽度之比为3:2.当通道总面积为花坛总面积的
如图,八一广场要设计一个矩形花坛,花坛的长、宽分别为200m、120m,花坛中有一横两纵的通道,横、纵通道的宽度之比为3:2.当通道总面积为花坛总面积的

 时,求横、纵通道的宽分别是多少?
时,求横、纵通道的宽分别是多少?
 时,求横、纵通道的宽分别是多少?
时,求横、纵通道的宽分别是多少?