Question

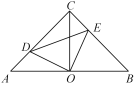
【题目】如图，在△ABC中，∠ACB＝90°，AC＝BC，O是AB的中点，点D在AC上，点E在BC上，且∠DOE＝90°.则下列结论：①OA＝OB＝OC；②CD＝BE；③△ODE是等腰直角三角形；④四边形CDOE的面积等于△ABC的面积的一半.其中正确的有____(填序号).

Answer 1

【答案】①②③④

【解析】

根据直角三角形斜边上的中线等于斜边的一半来判定①；证明△COD≌△BOE，来判定②③④；

解：在△ABC中，∵∠ACB＝90°，AC＝BC，O是AB的中点，

∴OA＝OB＝OC；故①正确；

∵AC＝BC，O是AB的中点，∴OC⊥AB,

∵∠DOE＝∠COB=90°

∴∠DOC=∠EOB,

又∵OC=OB,∠DCO=∠EBO=45°，

∴△COD≌△BOE．

∴CD=EB,OD=OE,S△COD =S△BOE,即②③④正确.

故答案为：①②③④.