题目内容
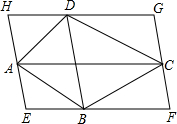 如图,过四边形ABCD的四个顶点分别作对角线AC、BD的平行线,若所围成的四边形EFGH是矩形时,原四边形ABCD必须满足的条件是
如图,过四边形ABCD的四个顶点分别作对角线AC、BD的平行线,若所围成的四边形EFGH是矩形时,原四边形ABCD必须满足的条件是
- A.AD⊥CD
- B.AD=CD
- C.AC⊥BD
- D.AC=BD
C
分析:根据平行公理的推论求出EF∥GH,EH∥FG,推出平行四边形EFGH,证出∠E=90°即可.
解答: 解:添加的条件是AC⊥BD,
解:添加的条件是AC⊥BD,
∵BD∥EF,BD∥GH,
∴EF∥GH,
同理EH∥GF,
∴四边形EFGH是平行四边形,
∵EF∥BD,AC⊥BD,
∴EF⊥AC,
∵EH∥AC,
∴EF⊥EH,
∴∠E=90°,
∴平行四边形EFGH是矩形,
故选:C.
点评:此题主要考查了矩形的判定,平行四边形的判定,平行公理及推论等知识点的理解和掌握,能求出平行四边形EFHGH和∠E=90°是解此题的关键.
分析:根据平行公理的推论求出EF∥GH,EH∥FG,推出平行四边形EFGH,证出∠E=90°即可.
解答:
 解:添加的条件是AC⊥BD,
解:添加的条件是AC⊥BD,∵BD∥EF,BD∥GH,
∴EF∥GH,
同理EH∥GF,
∴四边形EFGH是平行四边形,
∵EF∥BD,AC⊥BD,
∴EF⊥AC,
∵EH∥AC,
∴EF⊥EH,
∴∠E=90°,
∴平行四边形EFGH是矩形,
故选:C.
点评:此题主要考查了矩形的判定,平行四边形的判定,平行公理及推论等知识点的理解和掌握,能求出平行四边形EFHGH和∠E=90°是解此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
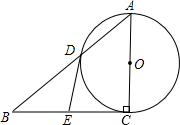 ,交BC于点E.
,交BC于点E.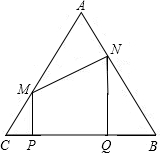 边,PQ=1,过点P作PM⊥CB,交AC于M,过点Q作QN⊥CB,交AB于N,连接MN.记CP的长为t.
边,PQ=1,过点P作PM⊥CB,交AC于M,过点Q作QN⊥CB,交AB于N,连接MN.记CP的长为t.
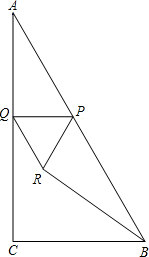 (2012•平顶山一模)如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=10,P是AB边上的一个动点(异于A、B两点),过点P作PQ⊥AC于Q,以PQ为边向下作等边三角形PQR.设AP=x,△PQR与△ABC重叠部分的面积为y,连接RB.
(2012•平顶山一模)如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=10,P是AB边上的一个动点(异于A、B两点),过点P作PQ⊥AC于Q,以PQ为边向下作等边三角形PQR.设AP=x,△PQR与△ABC重叠部分的面积为y,连接RB.