题目内容
一个四边形的边长分别是3、4、5、6，另一个与它相似的四边形最小边长为6，则第二个四边形的周长是
36
36
．分析：先求出已知四边形的周长，再根据相似多边形的周长的比等于相似比列式求解即可．
解答：解：3+4+5+6=18，
设第二个四边形的周长为x，
∵两个四边形相似，
∴
=
，
解得x=36．
故答案为：36．
设第二个四边形的周长为x，
∵两个四边形相似，
∴
| x |
| 18 |
| 6 |
| 3 |
解得x=36．
故答案为：36．
点评：本题考查了相似多边形的周长的比等于相似比，比较简单，要注意对应边的确定．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
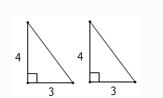29、如图，有两个全等的直角三角形，它们的边长分别为3和4，把这两个直角三角形拼成一个三角形或一个四边形，在这些图形中，周长最小值是
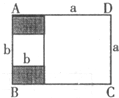20、如图，四边形ABCD是一个长方形，内有两个相邻的正方形，大、小正方形的边长分别为a、b．则图中阴影部分的面积为