题目内容
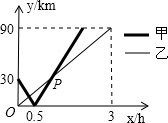 在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终达到C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.若两船的距离为10km时,甲行驶了
在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终达到C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.若两船的距离为10km时,甲行驶了分析:先根据一次函数的图象求出A、C两港之间的距离及乙的速度,再根据甲在乙船前和乙船后,及甲船已经到了而乙船正在行驶,三种情况进行解答即可.
解答:解:由函数图象可知,乙船的速度为:
=30km/小时,
①甲在乙后10km,设行驶时间为x,
甲从A行驶了60xkm,乙从B行驶了30xkm,
甲在B港后(30-60x)Km,乙在B港前 30x Km,甲乙相距10Km.
由 (30-60x)+30x=10,
得x=
;
②甲超过乙后,甲在乙前 10Km,设行驶时间为x,
甲从A行驶了60xKm(已超过了B港),乙从B行驶了30xkm,
乙在B港前 30xkm,甲在乙前10km处.
由60x-30-30x=10,
解得x=
(小时).
③甲船已经到了而乙船正在行驶,
∵90-30x=10,解得x=
(小时),
故答案为:
或
或
.
| 90 |
| 3 |
①甲在乙后10km,设行驶时间为x,
甲从A行驶了60xkm,乙从B行驶了30xkm,
甲在B港后(30-60x)Km,乙在B港前 30x Km,甲乙相距10Km.
由 (30-60x)+30x=10,
得x=
| 2 |
| 3 |
②甲超过乙后,甲在乙前 10Km,设行驶时间为x,
甲从A行驶了60xKm(已超过了B港),乙从B行驶了30xkm,
乙在B港前 30xkm,甲在乙前10km处.
由60x-30-30x=10,
解得x=
| 4 |
| 3 |
③甲船已经到了而乙船正在行驶,
∵90-30x=10,解得x=
| 8 |
| 3 |
故答案为:
| 2 |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
点评:本题考查的是一次函数的图象及一次函数的应用,解答此题时要注意运用分类讨论的思想,不要漏解.

练习册系列答案
相关题目
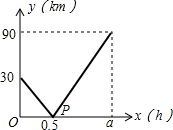 (2013•溧水县一模)在一条直线上依次有A、B、C三个海岛,某海巡船从A岛出发沿直线匀速经B岛驶向C岛,执行海巡任务,最终达到C岛.设该海巡船行驶x(h)后,与B港的距离为y(km),y与x的函数关系如图所示.
(2013•溧水县一模)在一条直线上依次有A、B、C三个海岛,某海巡船从A岛出发沿直线匀速经B岛驶向C岛,执行海巡任务,最终达到C岛.设该海巡船行驶x(h)后,与B港的距离为y(km),y与x的函数关系如图所示. (2013•滨湖区二模)在一条直线上依次有A、B、C三个海岛,某海巡船从A岛出发沿直线匀速经B 岛驶向C岛,执行海巡任务,最终达到C岛.设该海巡船行驶x(h)后,与B港的距离为y(km),y与x的函数关系如图所示.
(2013•滨湖区二模)在一条直线上依次有A、B、C三个海岛,某海巡船从A岛出发沿直线匀速经B 岛驶向C岛,执行海巡任务,最终达到C岛.设该海巡船行驶x(h)后,与B港的距离为y(km),y与x的函数关系如图所示. 终达到C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.
终达到C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.