题目内容
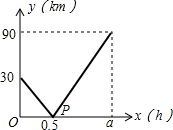 (2013•溧水县一模)在一条直线上依次有A、B、C三个海岛,某海巡船从A岛出发沿直线匀速经B岛驶向C岛,执行海巡任务,最终达到C岛.设该海巡船行驶x(h)后,与B港的距离为y(km),y与x的函数关系如图所示.
(2013•溧水县一模)在一条直线上依次有A、B、C三个海岛,某海巡船从A岛出发沿直线匀速经B岛驶向C岛,执行海巡任务,最终达到C岛.设该海巡船行驶x(h)后,与B港的距离为y(km),y与x的函数关系如图所示.(1)图中点P的坐标为(0.5,0),请解释该点坐标所表示的实际意义;
(2)填空:A、C两港口间的距离为
120
120
km,a=2
2
;当0<x≤0.5时,y与x的函数关系式为:
y=-60x+30
y=-60x+30
;当0.5<x≤a时,y与x的函数关系式为:
y=60x-30
y=60x-30
;(3)在B岛有一不间断发射信号的信号发射台,发射的信号覆盖半径为24km,求该海巡船能接受到该信号的时间有多长?
(4)请你根据以上信息,针对A岛,就该海巡船航行的“路程”,提出一个问题,并写出解答过程.
分析:(1)根据到B岛的距离为0可知点P表示达到B岛;
(2)A、C两港口间的距离等于A、C到B岛的距离之和;先根据速度=路程÷时间求出船的速度,然后再根据时间=路程÷速度列式计算即可求出a的值;
根据与B港的距离等于A、B两港间的距离减去船行驶的距离,列式整理即可;
根据路程=速度×时间列式整理即可得解;
(3)求出船距离B港24km时的时间,然后相减即可得解;
(4)出发1小时距离A港的距离.
(2)A、C两港口间的距离等于A、C到B岛的距离之和;先根据速度=路程÷时间求出船的速度,然后再根据时间=路程÷速度列式计算即可求出a的值;
根据与B港的距离等于A、B两港间的距离减去船行驶的距离,列式整理即可;
根据路程=速度×时间列式整理即可得解;
(3)求出船距离B港24km时的时间,然后相减即可得解;
(4)出发1小时距离A港的距离.
解答:解:(1)P点坐标的意义为:该海巡船出发0.5 h后,到达B岛;
(2)30+90=120千米,
船的速度为:
=60千米/小时,
a=120÷60=2;
当0<x≤0.5时,y=-60x+30,
当0.5<x≤2时,y=60(x-0.5)=60x-30,
即y=60x-30;
(3)由-60x+30=24,得:x=0.1,
由60x-30=24,得,x=0.9,
0.9-0.1=0.8小时,
所以,该海巡船能接受到该信号的时间为0.8小时;
(4)答案不唯一:例如,该海巡船1小时弧距离A岛有多少路程?
把x=1代入y=60x-30得,y=60-30=30千米.
故答案为:120,2;y=-60x+30,y=60x-30.
(2)30+90=120千米,
船的速度为:
| 30 |
| 0.5 |
a=120÷60=2;
当0<x≤0.5时,y=-60x+30,
当0.5<x≤2时,y=60(x-0.5)=60x-30,
即y=60x-30;
(3)由-60x+30=24,得:x=0.1,
由60x-30=24,得,x=0.9,
0.9-0.1=0.8小时,
所以,该海巡船能接受到该信号的时间为0.8小时;
(4)答案不唯一:例如,该海巡船1小时弧距离A岛有多少路程?
把x=1代入y=60x-30得,y=60-30=30千米.
故答案为:120,2;y=-60x+30,y=60x-30.
点评:本题考查的是用一次函数解决实际问题,本题主要利用了路程、速度、时间三者之间的关系,难度不大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2013•溧水县一模)如图,用圆心角为120°,半径为6cm的扇形纸片卷成一个圆锥形无底纸帽,则这个纸帽的高是
(2013•溧水县一模)如图,用圆心角为120°,半径为6cm的扇形纸片卷成一个圆锥形无底纸帽,则这个纸帽的高是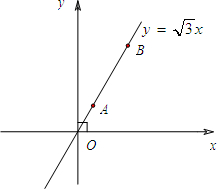 (2013•溧水县一模)如图,在平面直角坐标系中,A、B为正比例函数
(2013•溧水县一模)如图,在平面直角坐标系中,A、B为正比例函数