题目内容
【题目】如图，在
中，
平分
交
于点
的垂直平分线
交
于点
，交
于点
，若
，则的长为__________．
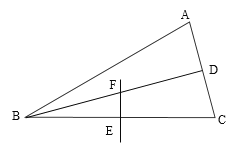
【答案】6
【解析】
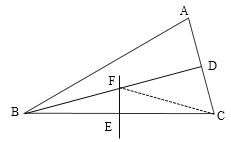
连接CF，根据等腰三角形的性质，得到∠ABD=∠CBD=15°，BD⊥AC，AD=CD，再由垂直平分线的性质得到BF=CF=6，再根据三角形的外角的性质得到∠CFD=∠CBD+∠BCF=30°，由30°的直角三角形的性质得出CD，即可求出AC的长度．
解：连接CF，∵
，BD是∠ABC的平分线，
，
∴∠ABD=∠CBD=15°，BD⊥AC，AD=CD
∵EF垂直平分BC，
∴BF=CF=6
∴∠CBD=∠BCF=15°，
∴∠CFD=∠CBD+∠BCF=30°，
∴在Rt△CFD中，CD=
，
∴AC=2CD=6，
故答案为：6．
练习册系列答案
相关题目
