题目内容
(2012•普陀区一模)在平面直角坐标系中,△ABC的顶点分别是A(-1,0),B(3,0),C(0,2),已知动直线y=m(0<m<2)与线段AC、BC分别交于D、E两点,而在x轴上存在点P,使得△DEP为等腰直角三角形,那么m的值等于
或1
或1.
| 4 |
| 3 |
| 4 |
| 3 |
分析:因为△ABC的顶点分别为A(-1,0),B(3,0),C(0,2),动直线y=m(0<m<2)与线段AC,BC分别交于D,E,要使△DEP为等腰直角三角形,(1)DE=EP,(或DP),∠DEP(或∠EDP)=90°或(2)PD=PE,∠EPD=90°,由直线方程和等腰直角三角形的性质及勾股定理求解.
解答:解:△DEP为等腰直角三角形分两种情况:
(1))DE=EP,(或DP),∠DEP(或∠EDP)=90°时,
设D(x1,m),E(x2,m),
∴(x1-x2) 2=m2,
由已知得CA方程:y=2x+2,
∴x1=
=
-1,
CB方程:y=-
x+2,
∴x2=-
=-
+3,
∴得:4(m-2)2=m2,
解得:m1=
,m2=4(与0<m<2不符舍去),
∴m=
;
(2)PD=PE,∠EPD=90°时,
则(
)2=m2,
∴( x2-x1)2=4m2,
∴4(m-2)2=4m2,
解得:m=1,
综上:当m=
或m=1时,△DEP为等腰直角三角形,故答案为:
或1.
(1))DE=EP,(或DP),∠DEP(或∠EDP)=90°时,
设D(x1,m),E(x2,m),
∴(x1-x2) 2=m2,
由已知得CA方程:y=2x+2,
∴x1=
| m-2 |
| 2 |
| m |
| 2 |
CB方程:y=-
| 2 |
| 3 |
∴x2=-
| 3(m-2) |
| 2 |
| 3m |
| 2 |
∴得:4(m-2)2=m2,
解得:m1=
| 4 |
| 3 |
∴m=
| 4 |
| 3 |
(2)PD=PE,∠EPD=90°时,
则(
| x2-x1 |
| 2 |
∴( x2-x1)2=4m2,
∴4(m-2)2=4m2,
解得:m=1,
综上:当m=
| 4 |
| 3 |
| 4 |
| 3 |
点评:此题考查的知识点是等腰直角三角形的性质运用及坐标与图形的性质,关键是确定等腰直角三角形的两种情况,然后分别求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•普陀区一模)如图,由5个同样大小的正方形合成一个矩形,那么∠ABD+∠ADB的度数是( )
(2012•普陀区一模)如图,由5个同样大小的正方形合成一个矩形,那么∠ABD+∠ADB的度数是( )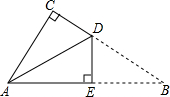 (2012•普陀区一模)如图是一张直角三角形的纸片,直角边AC=6cm,
(2012•普陀区一模)如图是一张直角三角形的纸片,直角边AC=6cm,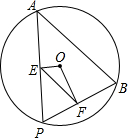 (2012•普陀区一模)如图,点A,B是⊙O上两点,AB=10,点P是⊙O上的动点(P与A,B不重合),连接AP,BP,过点O分别作OE⊥AP,OF⊥BP,点E、F分别是垂足.
(2012•普陀区一模)如图,点A,B是⊙O上两点,AB=10,点P是⊙O上的动点(P与A,B不重合),连接AP,BP,过点O分别作OE⊥AP,OF⊥BP,点E、F分别是垂足.