题目内容
如图，在直角坐标系中，矩形OABC的顶点A、B在双曲线y=kx(x＞0)上，BC与x轴交于点D．若点A的坐标为(1，2)，则点B的坐标为_________.
B（4，
）．
解析试题分析：由矩形OABC的顶点A、B在双曲线y=
（x＞0）上，BC与x轴交于点D．若点A的坐标为（1，2），利用待定系数法即可求得反比例函数与直线OA的解析式，又由OA⊥AB，可得直线AB的系数，继而可求得直线AB的解析式，将直线AB与反比例函数联立，即可求得点B的坐标．
试题解析：∵矩形OABC的顶点A、B在双曲线y=（x＞0）上，点A的坐标为（1，2），
∴2=
，
解得：k=2，
∴双曲线的解析式为：y=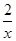
，直线OA的解析式为：y=2x，
∵OA⊥AB，
∴设直线AB的解析式为：y=-x+b，
∴2=-×1+b，
解得：b=
，
∴直线AB的解析式为：y=-x+，
将直线AB与反比例函数联立得出：
，
解得：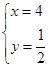 
或 
∴点B（4，）．
考点: 反比例函数综合题.
练习册系列答案
相关题目
上的点，A、B两点的横坐标分别是a、2a，线段AB的延长线交x轴于点C，若S△AOC＝6，则k的值为 ．
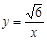上的一点，过点M作x轴、y轴的垂线，分别交直线y＝－x＋m于D、C两点，若直线y＝－x＋m与y轴、x轴分别交于点A、B，则AD•BC的值为 ；
（x＞0）上，以P为圆心的⊙P与两坐标轴都相切，点E为y轴负半轴上的一点，过点P作PF⊥PE交x轴于点F，若OF－OE＝6，则k的值是 ．
的图象上.反比例函数
的图象经过点C，交AB于点D，则点D的坐标是 .
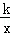在第二象限的交点，AB⊥OA交x轴于点B，△AOB的面积为4，则k的值是_____________.
（k＞0，x＞0）的图象上，过点A、B作x轴的垂线，垂足分别为M、N，延长线段AB交x轴于点C，若OM＝MN＝NC，△AOC的面积为6，则k的值为 . 
与
的图象的交点坐标为（a，b），则
的值为_________．