Question

【题目】如图，在矩形ABCD中，把∠B，∠D分别翻折，使点B，D分别落在对角线AC上的点E，F处，折痕分别为CM，AN．

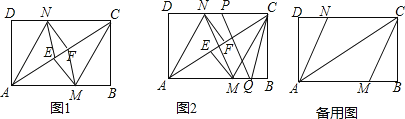
（1）求证：△AND≌△CMB；

（2）连接MF、NE，证明四边形MFNE是平行四边形；四边形MFNE是菱形吗？请说明理由；

（3）点P、Q是矩形的边CD、AB上的两点，连接PQ、CQ、MN，如图2所示，若PQ=CQ，PQ∥MN，且AB=4，BC=3，DN=，求PC的长度．

Answer 1

【答案】见解析

【解析】

试题分析：（1）根据折叠的性质得出∠DAN=∠NAC，∠BCM=∠ACM，从而根据AD∥BC可得出∠DAN=∠BCM，从而即可判断出△ADN≌△CBM．

（2）连接NE、MF，根据（1）的结论可得出NF=ME，再由∠NFE=∠MEF可判断出NF∥ME，在直角三角形NFE中，NE为斜边，NF为直角边，可判断四边形MFNE不是菱形．

（3）设AC与MN的交点为O，EF=x，作QG⊥PC于G点，首先求出AC=5，根据翻折变换知：AF=CE=3，于是可得AF+（CE﹣EF）=5，可得EF=1，在Rt△NFE中，NO2=NF2+OF2，求出NO的长，即NM=PQ=QC=2NO，PC=2．

（1）证明：∵四边形ABCD是正方形，

∴AD=BC，∠B=∠D=90°，

由折叠的性质得出∠DAN=∠NAC，∠BCM=∠ACM，

∵AD∥BC，

∴∠DAC=∠BCA，

∴∠DAN=∠BCM，

在Rt△AND和Rt△CMB中，，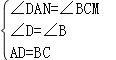

∵∴△AND≌△CMB（AAS）

（2）解：由（1）得：△AND≌△CMB，

∴NF=ME，

∵∠NFE=∠MEF，

∴NF∥ME，

∴四边形MFNE是平行四边形，

∵MN与EF不垂直，

∴四边形MFNE不是菱形；

（3）解：设AC与MN的交点为O，EF=x，作QG⊥PC于G点，如图所示：

∵AB=4，BC=3，

∴AC=5，

∵AF=CE=BC=3，

∴2AF﹣EF=AC，即6﹣x=5，

解得：x=1，

∴EF=1，

∴CF=2，

由折叠的性质得：NF=DN=，

∵OE=OF=EF=，

∴在Rt△NFO中，ON2=OF2+NF2，

∴ON=，

∴MN=2ON=，

∵PQ∥MN，PN∥MQ，

∴四边形MQPN是平行四边形，

∴MN=PQ=，

∵PQ=CQ，

∴△PQC是等腰三角形，

∴PG=CG，

在Rt△QPG中，PG2=PQ2﹣QG2，

∴PG==1，

∴PC=2PG=2．